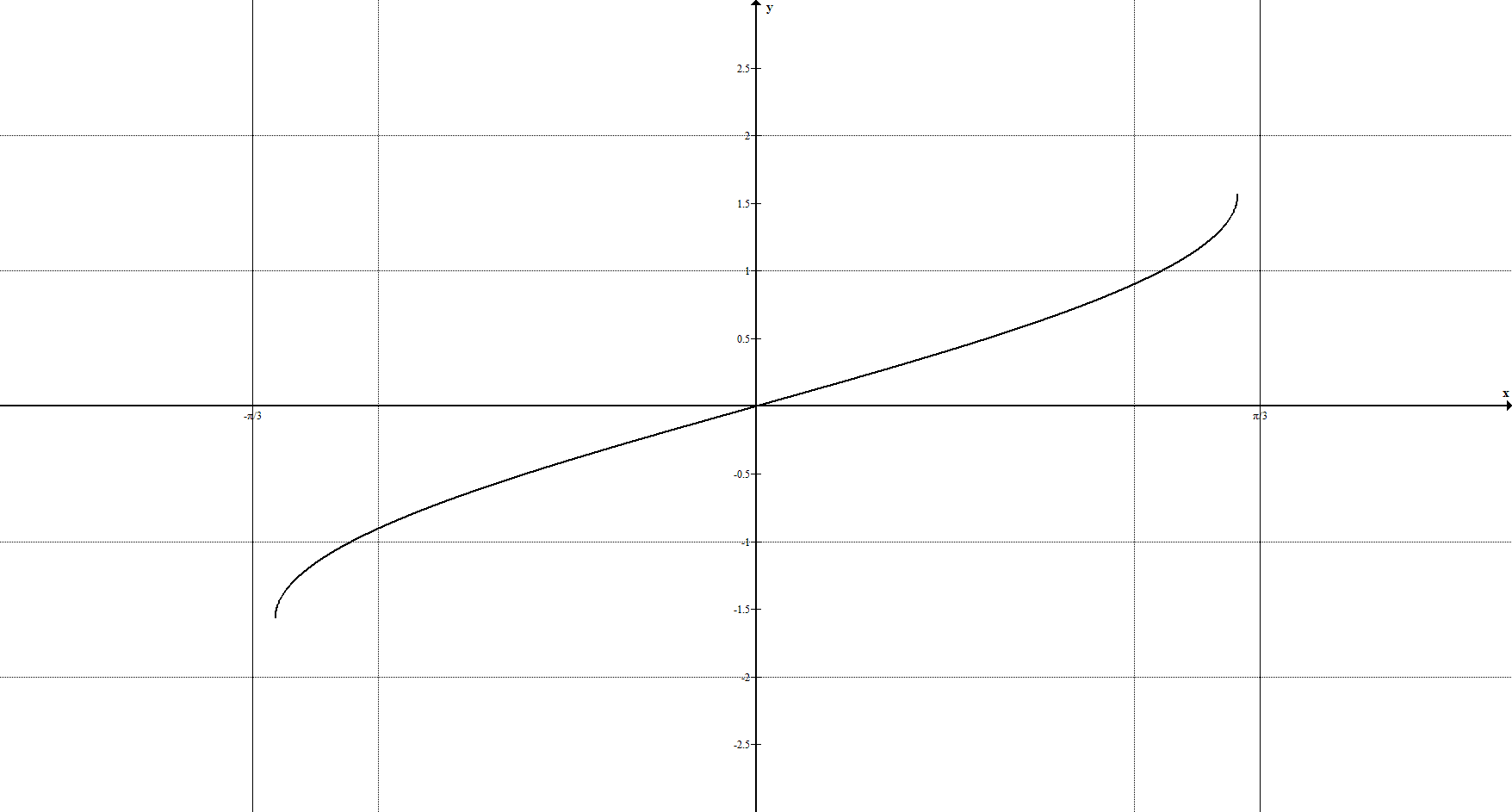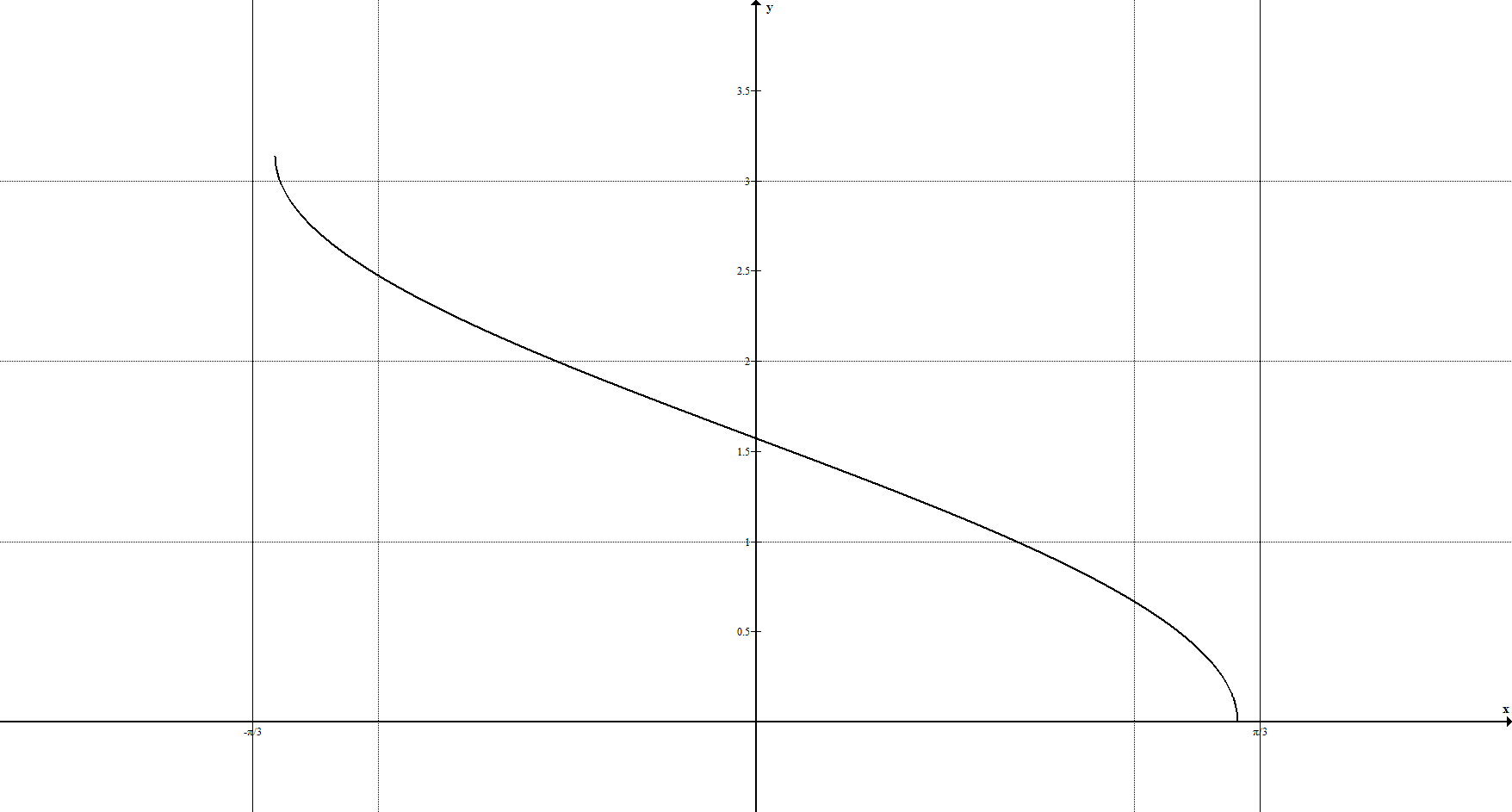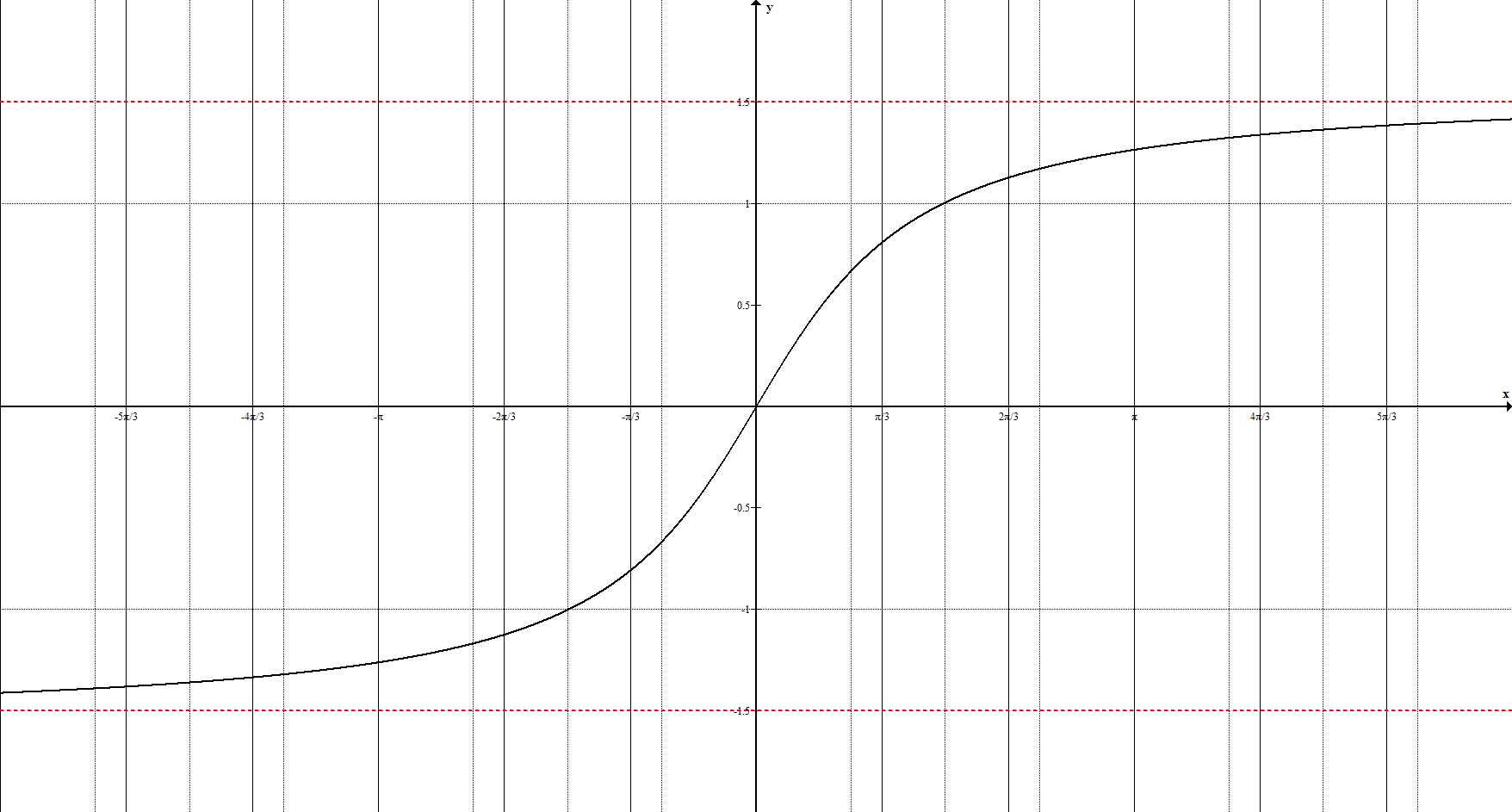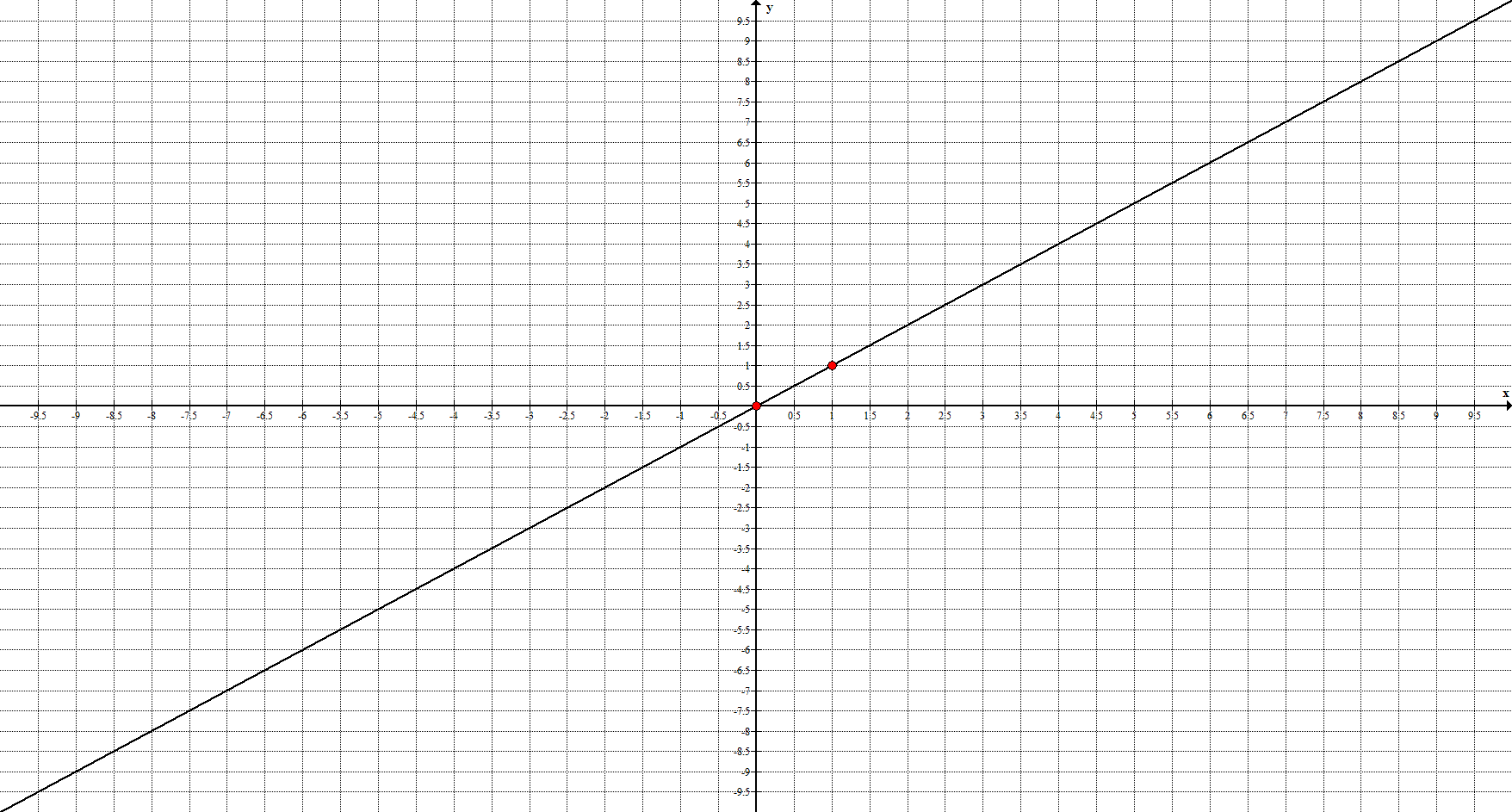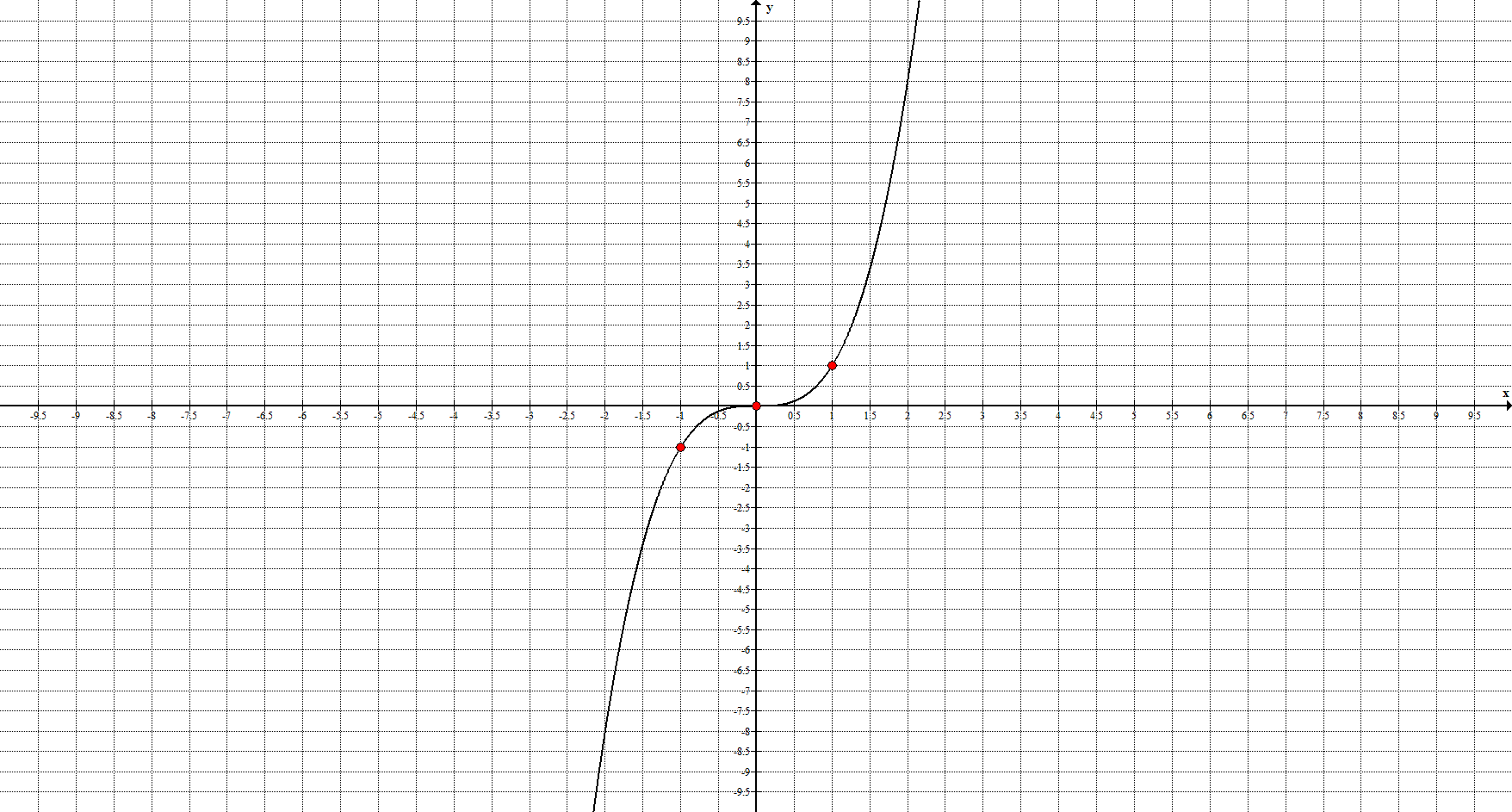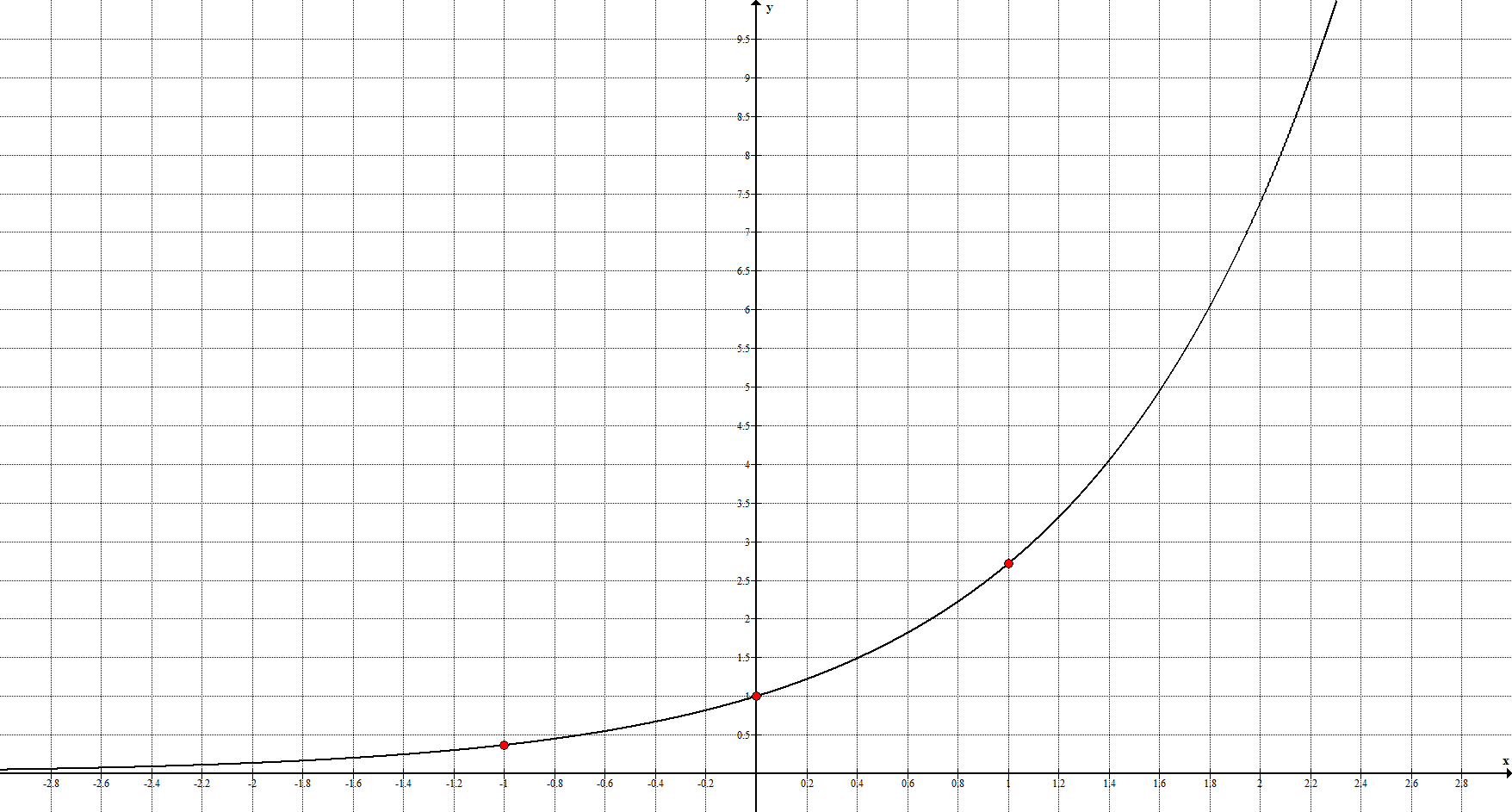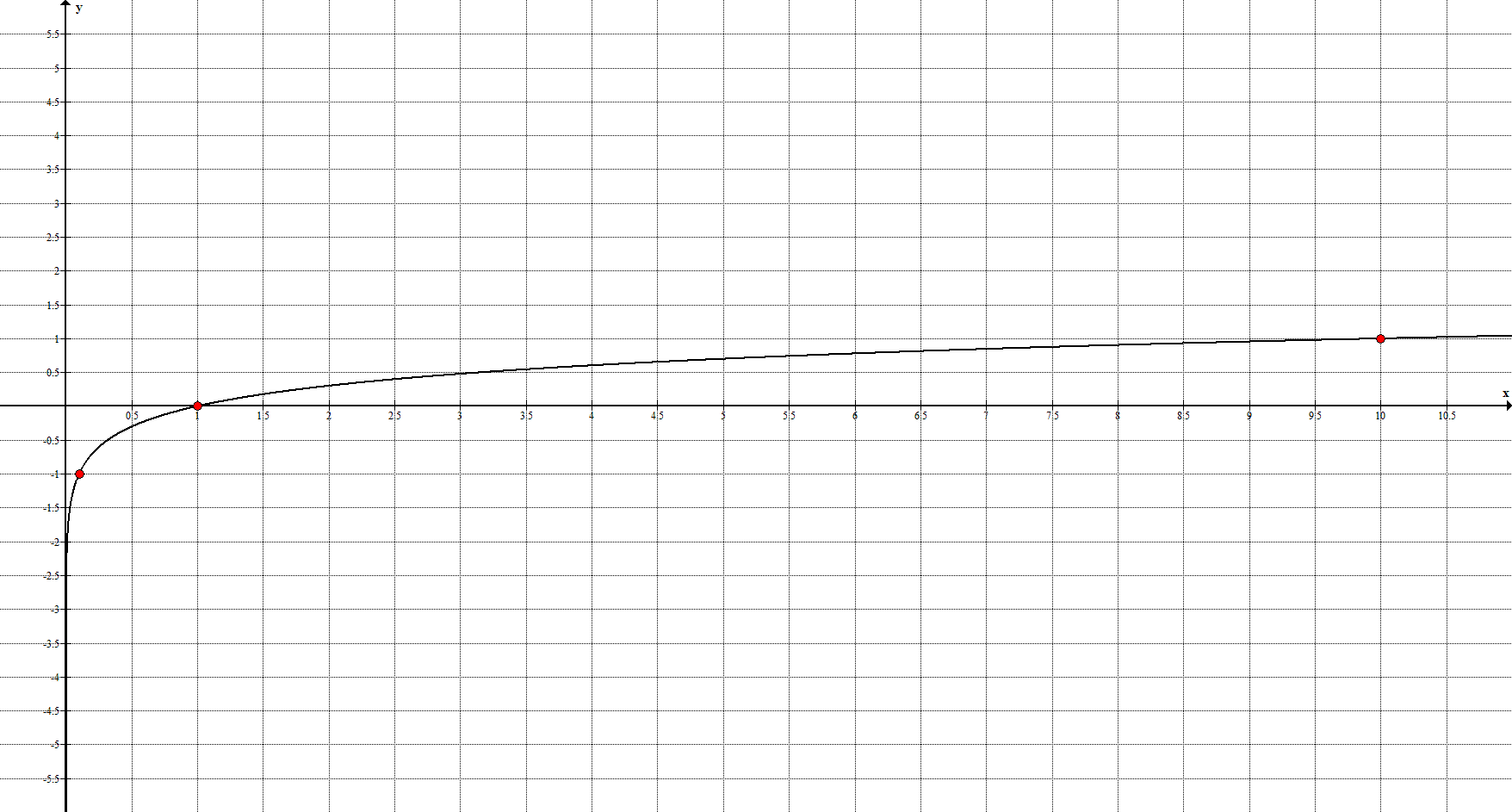Перед вами первая статья из цикла «Геометрические преобразования графиков функций«.
Набор функций, которые мы можем построить достаточно невелик. Однако, большинство функций строятся с помощью четырёх арифметических операций и суперпозиций (или, по-другому, комбинаций) основных элементарных функций.
К числу основных элементарных функций относятся:
1. Прямая задаётся уравнением $y=x$ и её график имеет вид:
Ключевые точки: $(0;0), \ (1;1)$
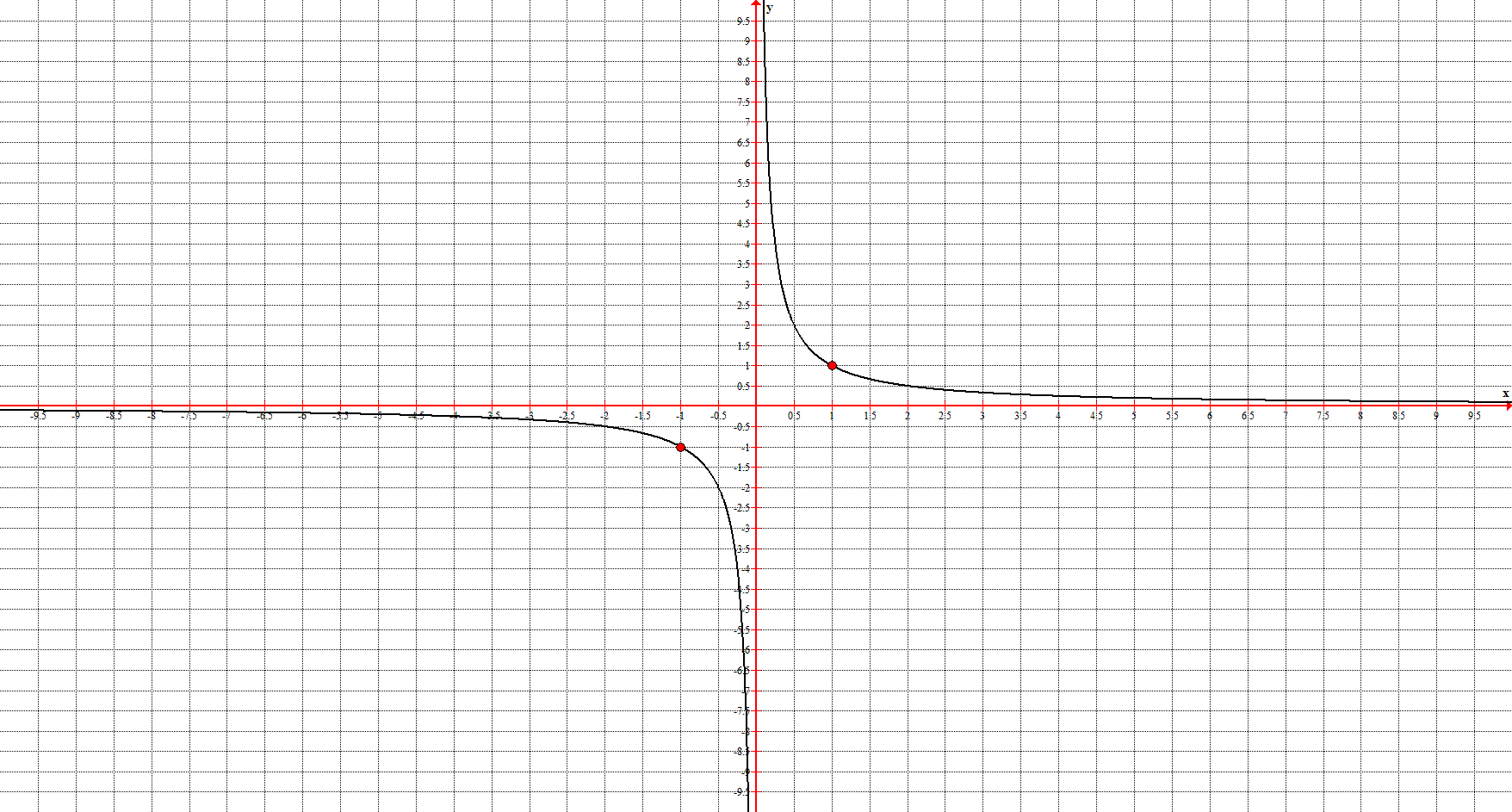
2. Гипербола (или обратная пропорциональность) задаётся уравнением $y=\frac{1}{x}$ и её график имеет вид:
Асимптоты: $x=0, \ y=0$
Ключевые точки: $(-1;1), \ (1;1)$
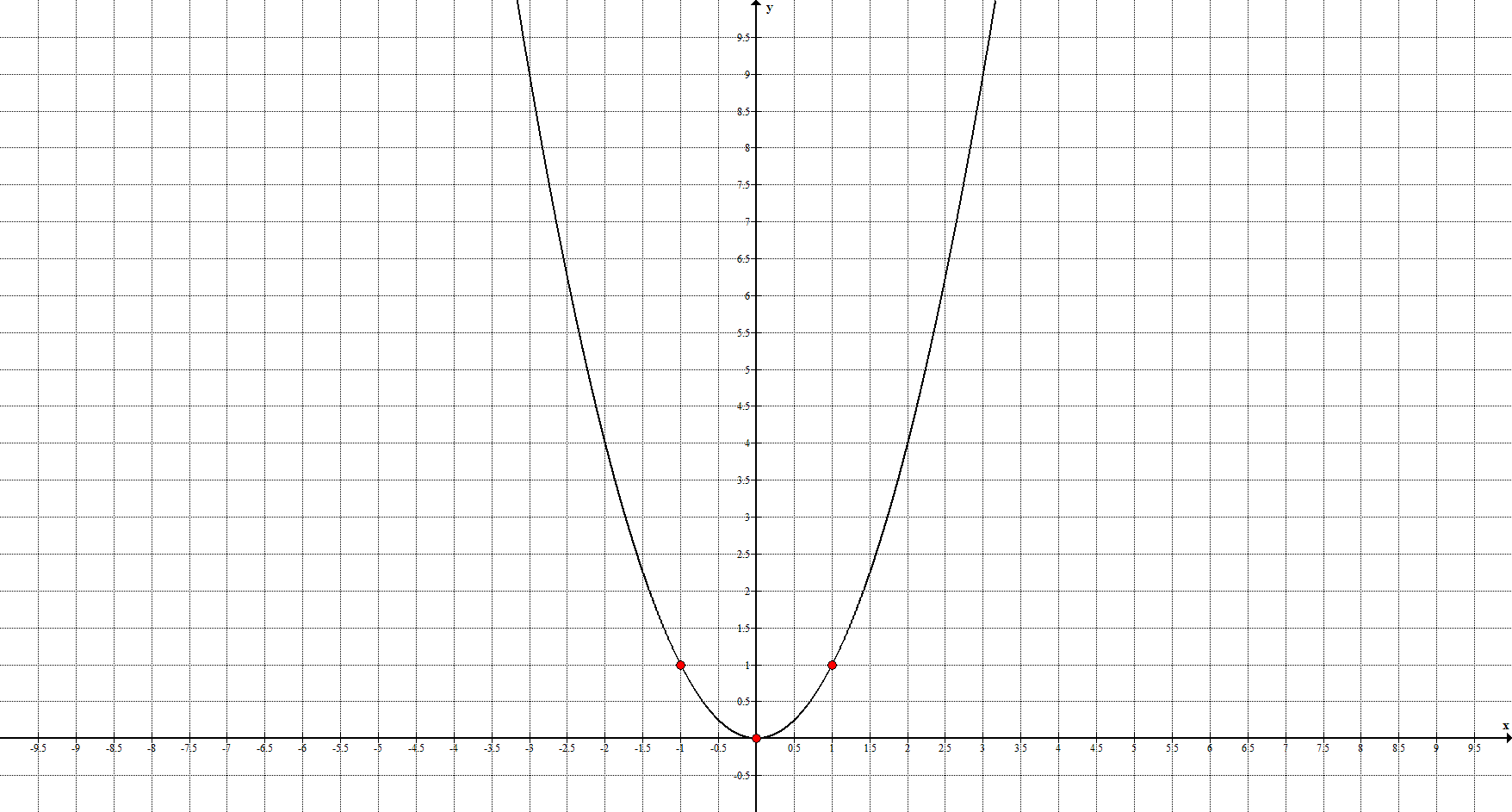
3. Парабола задаётся уравнением $y=x^2$ и её график имеет вид:
Ключевые точки: $(-1;1), \ (0;0), \ (1;1)$
4. Кубическая парабола задаётся уравнением $y=x^3$ и её график имеет вид:
Ключевые точки: $(-1;-1), \ (0;0), \ (1;1)$
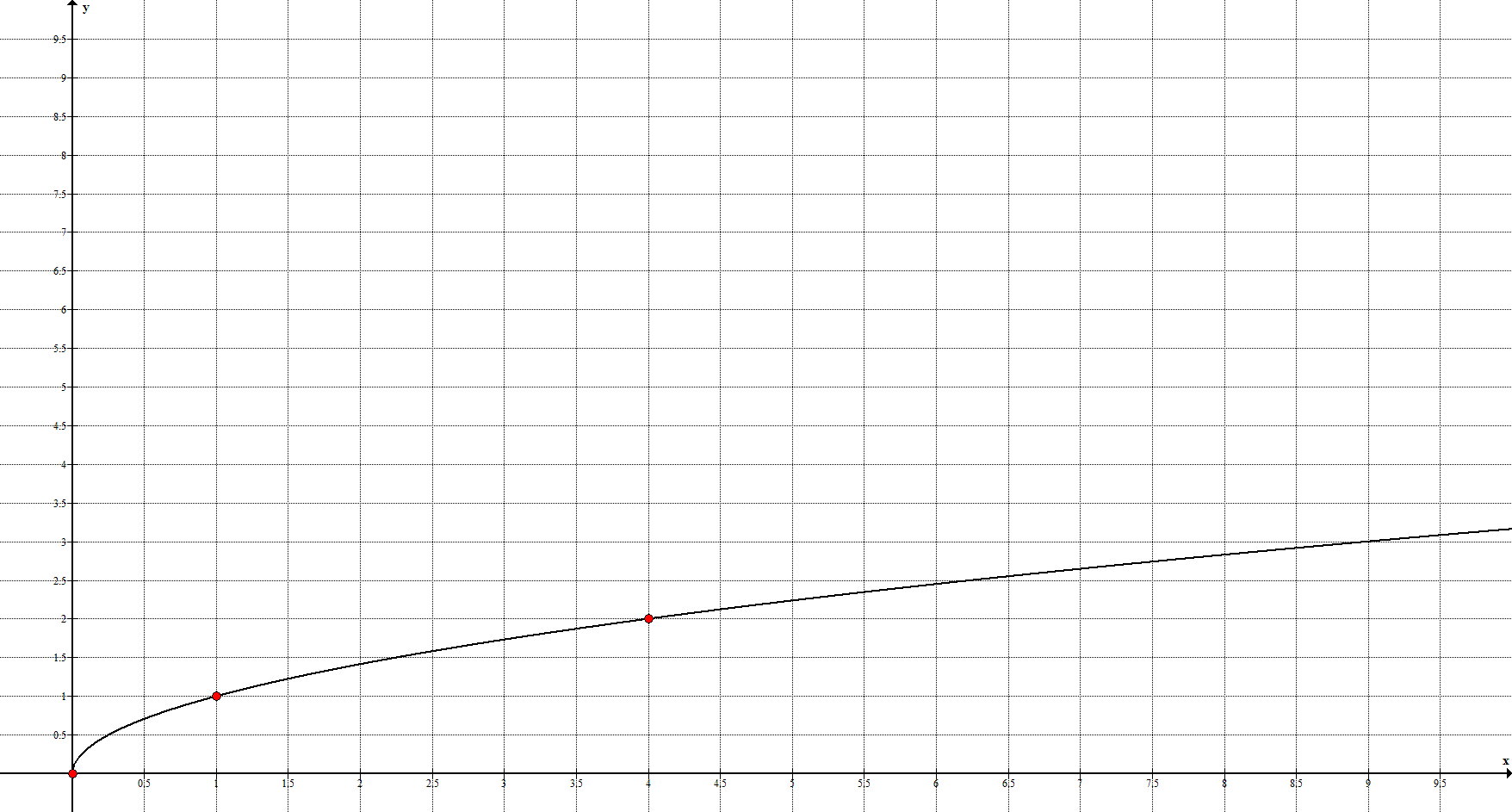
5. Коренная функция задаётся уравнением $y=\sqrt{x}$ и её график имеет вид:
Ключевые точки: $(0;0), \ (1;1), \ (4;2)$
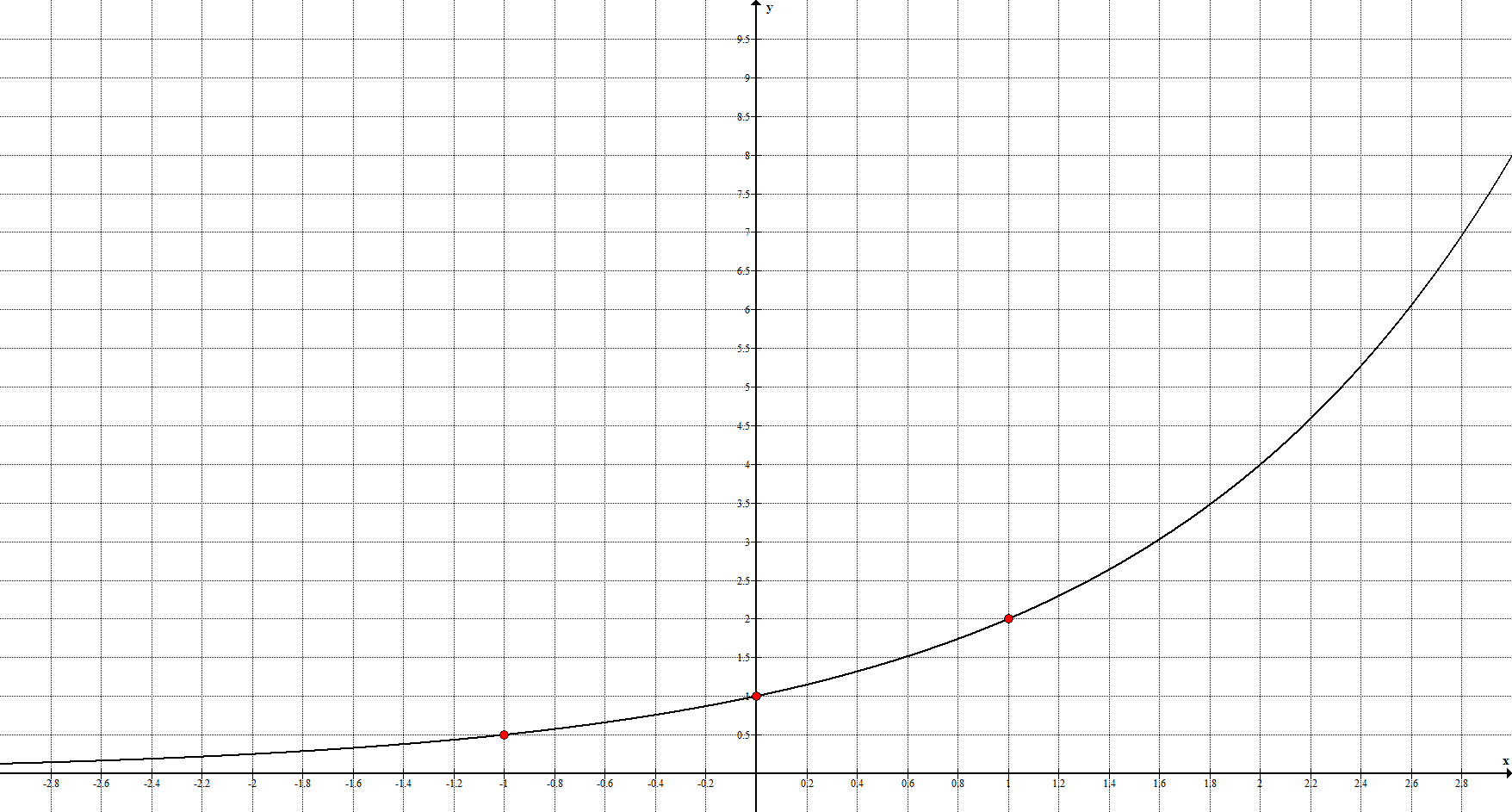
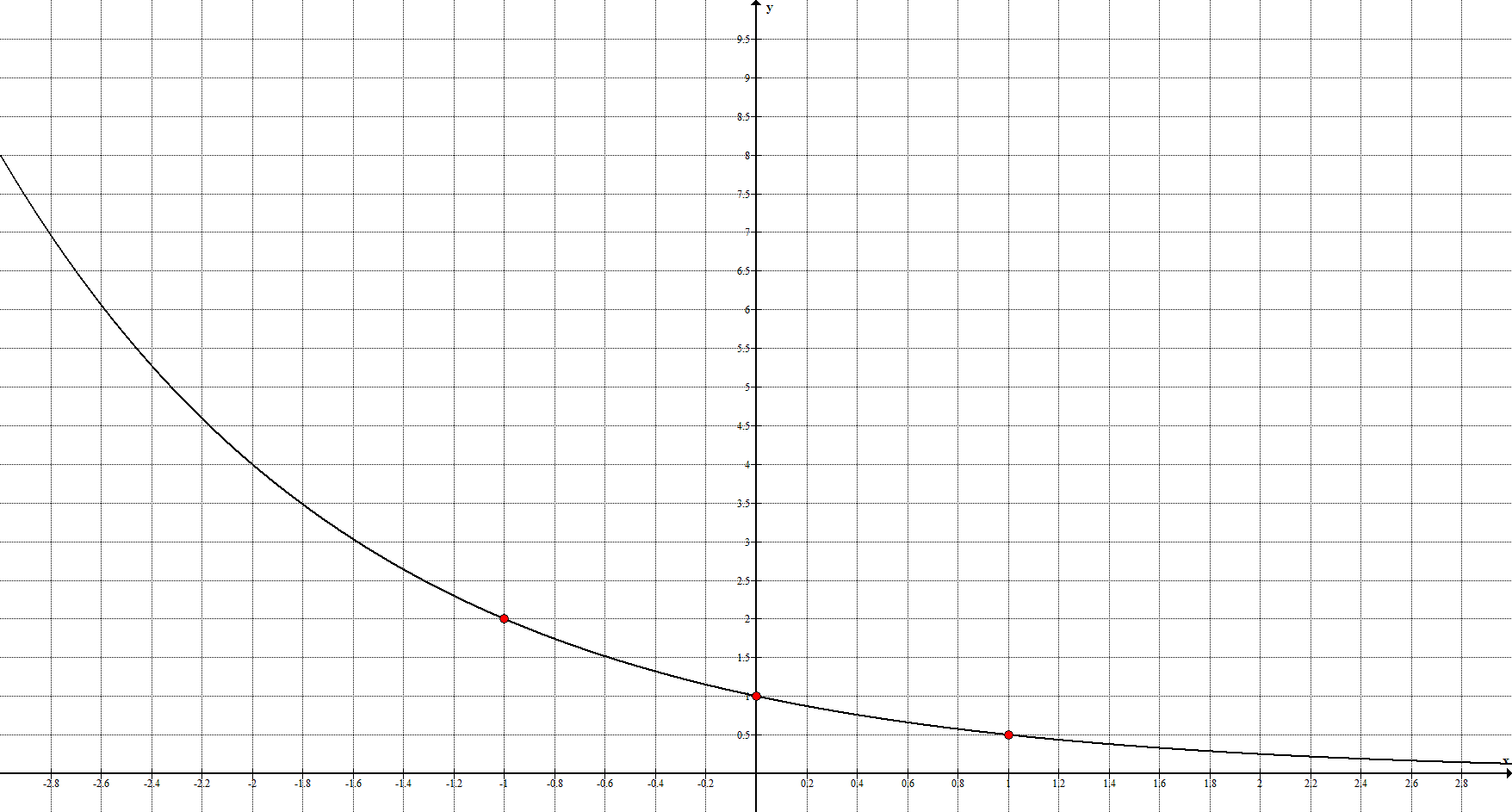
6. Показательная функция задаётся уравнением $y=a^{x}, \ a > 0, \ a \neq 1$ и её график имеет вид:
Ключевые точки: $\left(-1;\frac{1}{a}\right), \ (0;1), \ (1;a)$
6*. Экспонента (показательная функция с основанием e) задаётся уравнением $y=e^{x}$ и её график имеет вид:
Ключевые точки: $\left(-1;\frac{1}{e}\right), \ (0;1), \ (1;e)$
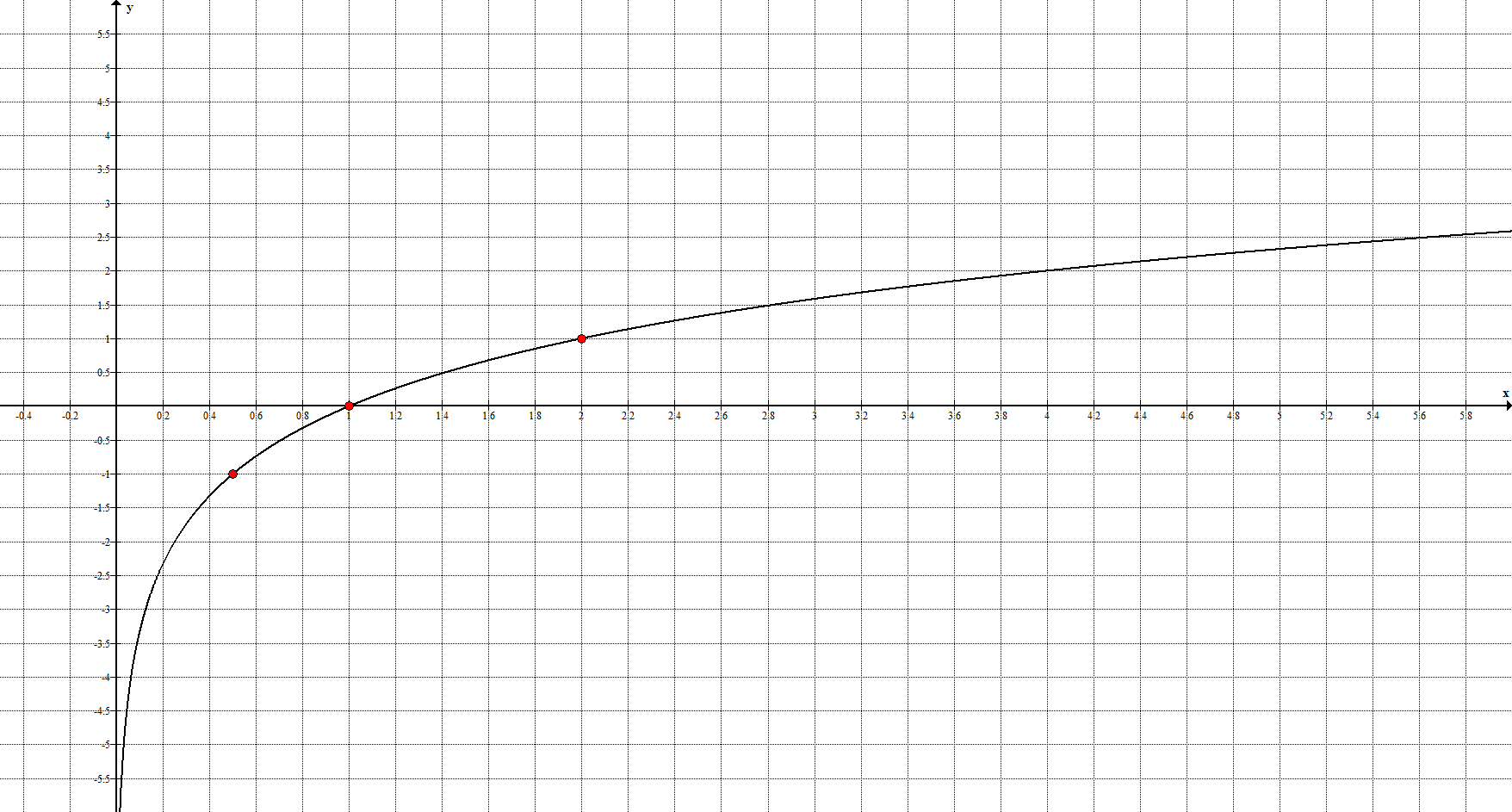
7. Логарифмическая функция задаётся уравнением $y=\log_{a}{x}, \ a > 0, \ a \neq 1$ и её график имеет вид:
Ключевые точки: $\left(\frac{1}{a}\right); -1), \ (0;1), \ (a;1)$
7*. Десятичный логарифм задаётся уравнением $y=\lg{x}$ и её график имеет вид:
Ключевые точки: $(0,1; -1), \ (0;1), \ (10;1)$
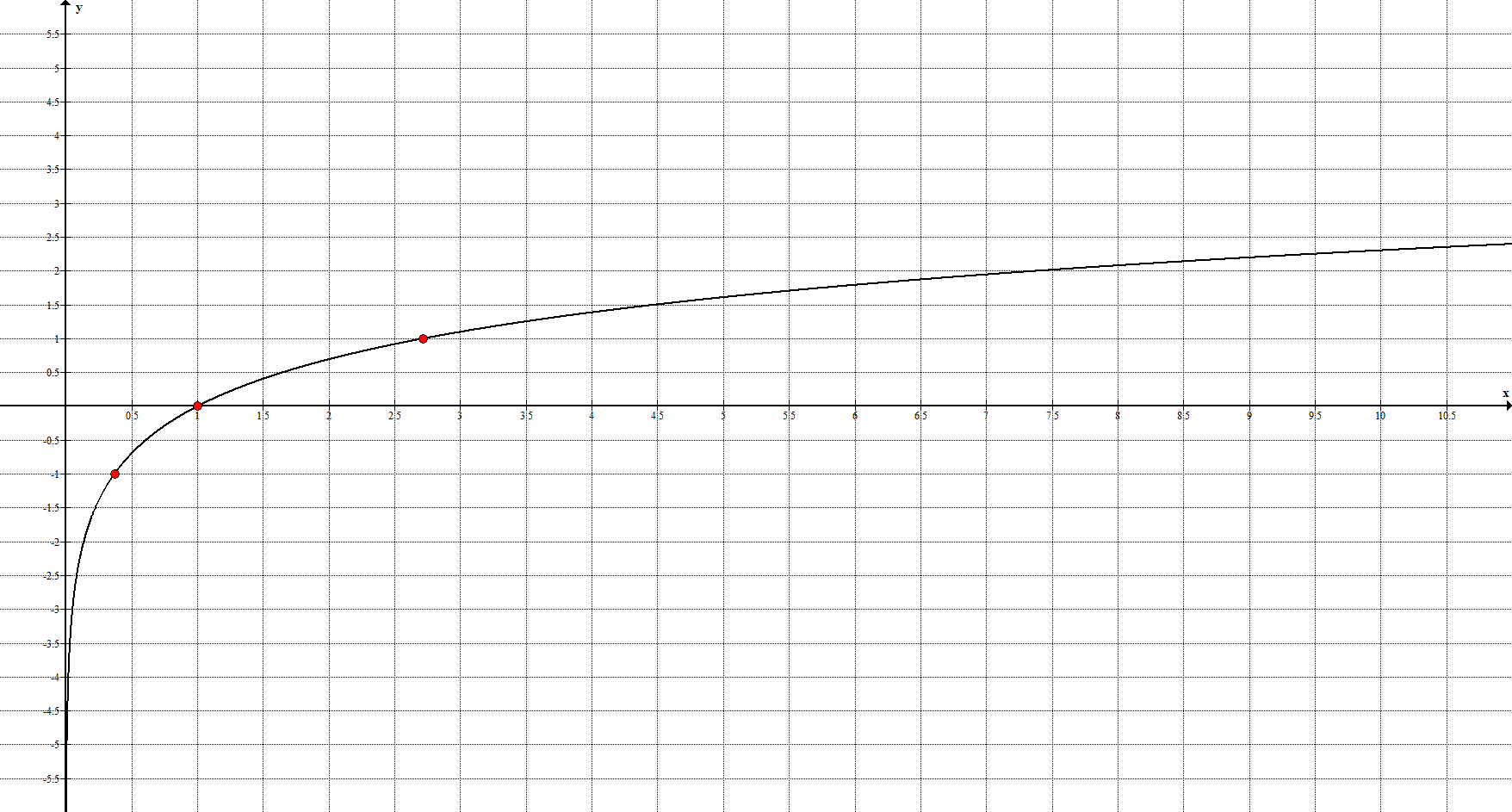
7**. Натуральный логарифм задаётся уравнением $y=\ln{x}$ и её график имеет вид:
Ключевые точки: $\left(\frac{1}{e}; -1\right), \ (0;1), \ (e;1)$
8. Тригонометрические функции задаются уравнением $y=\sin{x}, \ y=\cos{x}, \ y={\rm tg}{x}, \ y={\rm ctg}{x}$ и их графики имеют вид:
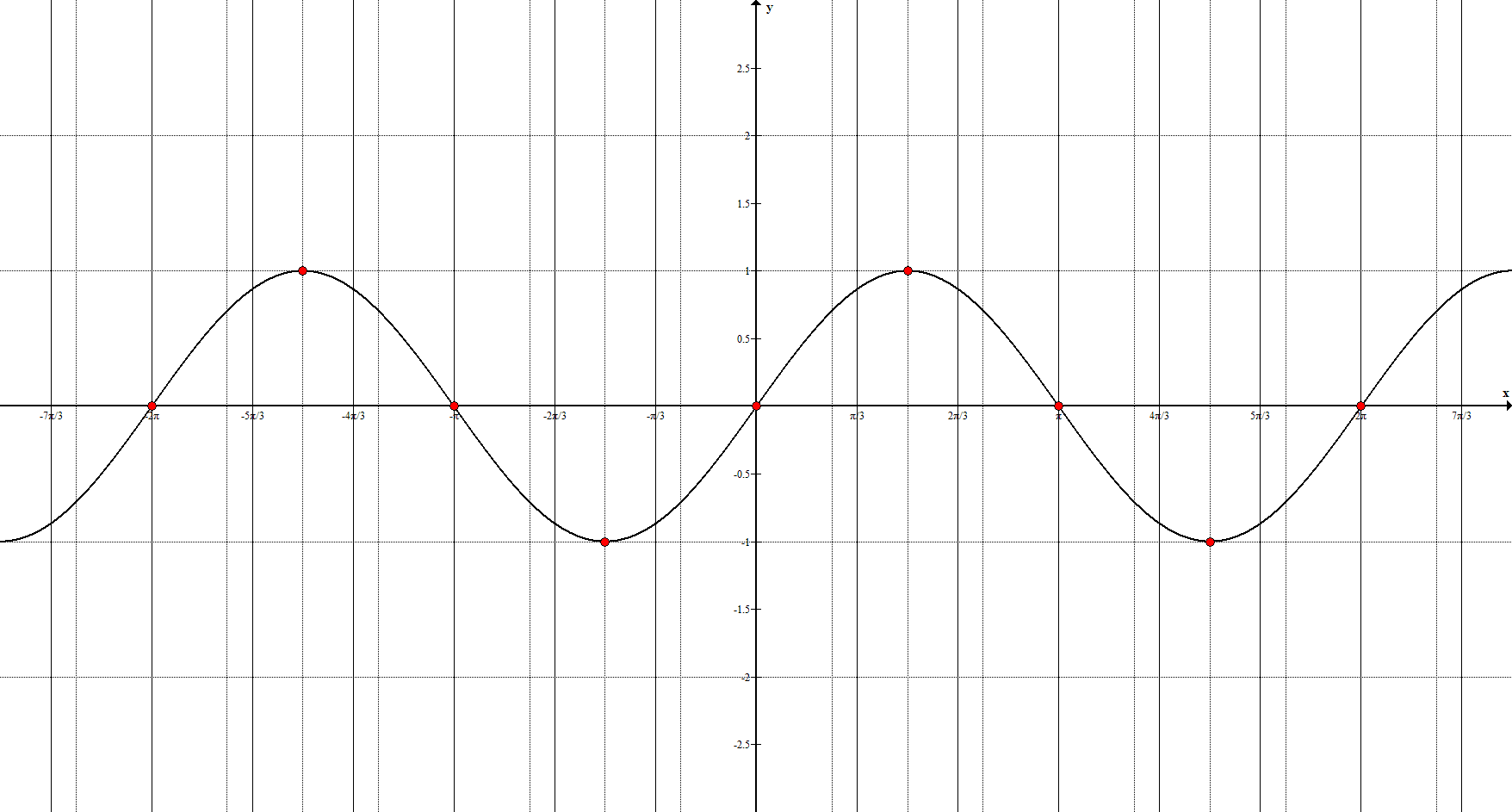
Ключевые точки: $(-2\pi; 0), \ \left(-\frac{3\pi}{2}; 1\right), \ (-\pi;0), $
$\left(-\frac{\pi}{2}; -1\right), \ (0;0), \ \left(\frac{\pi}{2}; 1\right), \ (\pi; 0), \ \left(\frac{3\pi}{2}; -1\right), \ (2\pi; 0)$
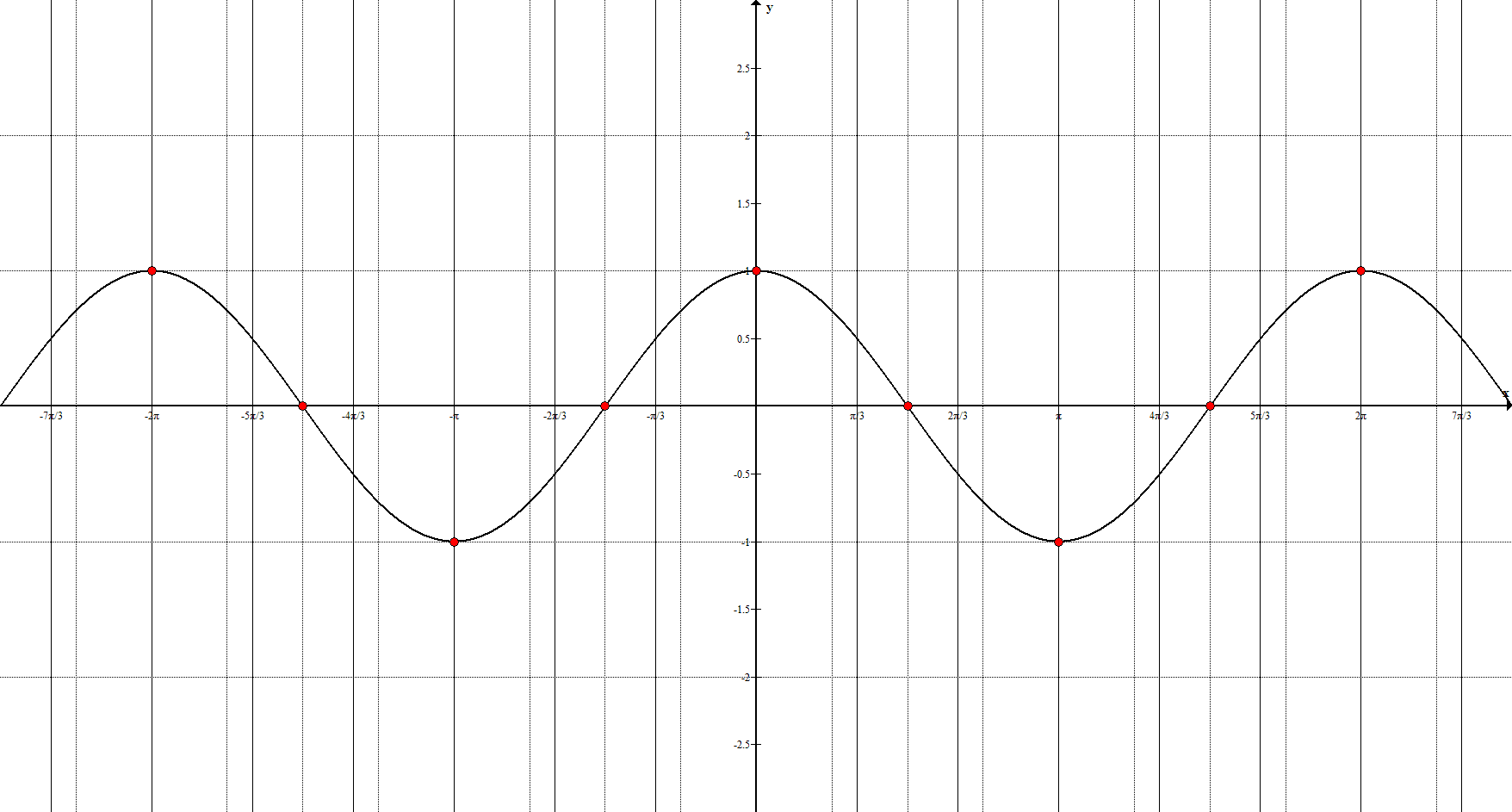
Ключевые точки: $(-2\pi; 1), \ \left(-\frac{3\pi}{2}; 0\right), \ (-\pi;-1), $
$\left(-\frac{\pi}{2}; 0\right), \ (0;1), \ \left(\frac{\pi}{2}; 0\right), \ (\pi;-1), \ \left(\frac{3\pi}{2}; 0\right), \ (2\pi; 1)$
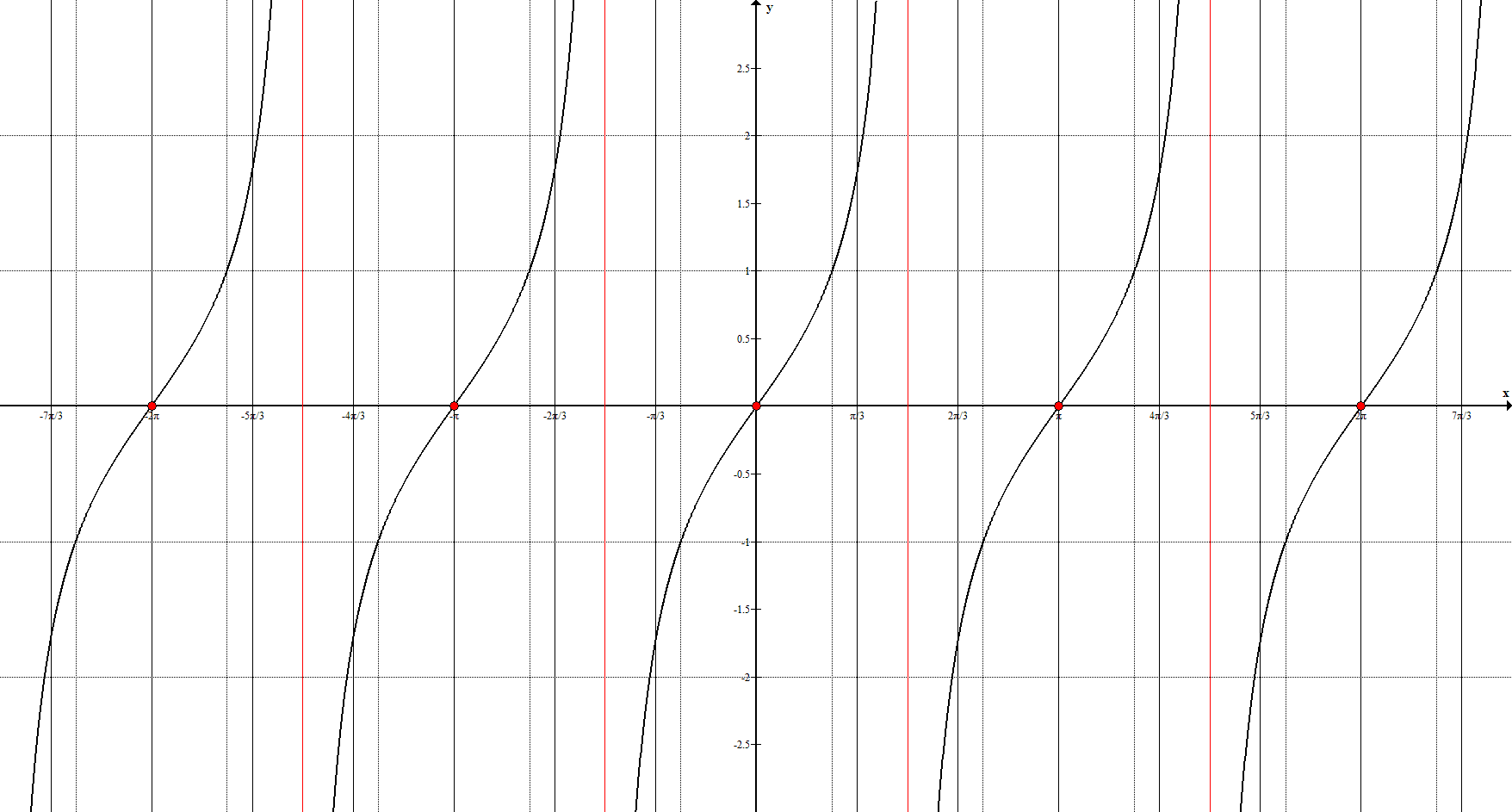
Асимптоты: $x=\frac{\pi}{2}+\pi n, n \in Z$
Ключевые точки: $(-2\pi ;0), \ (-\pi ;0), \ (0;0), \ (\pi ;0), \ (2\pi ;0)$
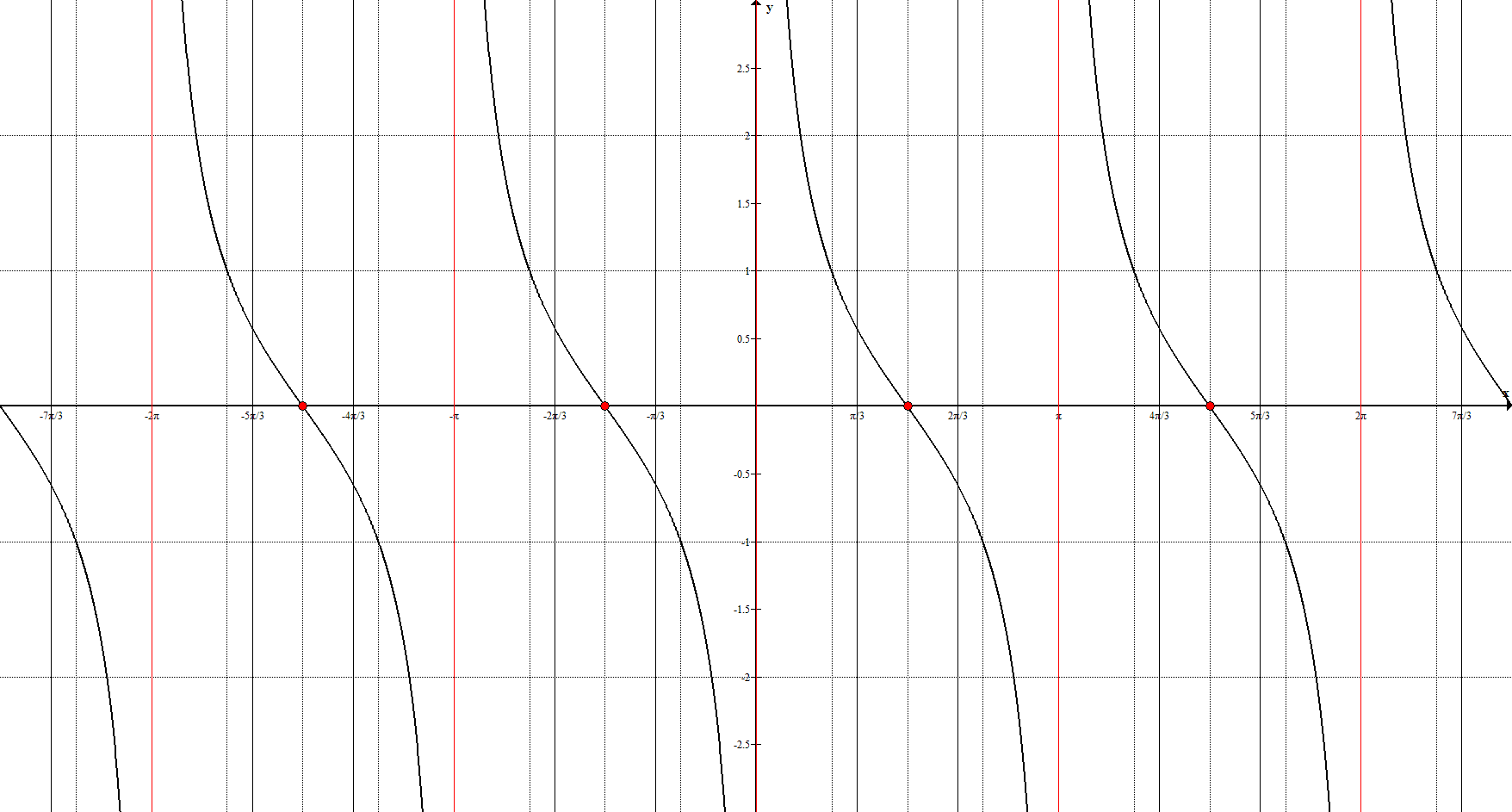
Асимптоты: $x=\pi n, n \in Z$
Ключевые точки: $\left(-\frac{3\pi}{2}; 0\right), \ \left(-\frac{\pi}{2}; 0\right), \ \left(\frac{\pi}{2}; 0\right), \ \left(\frac{3\pi}{2}; 0\right)$
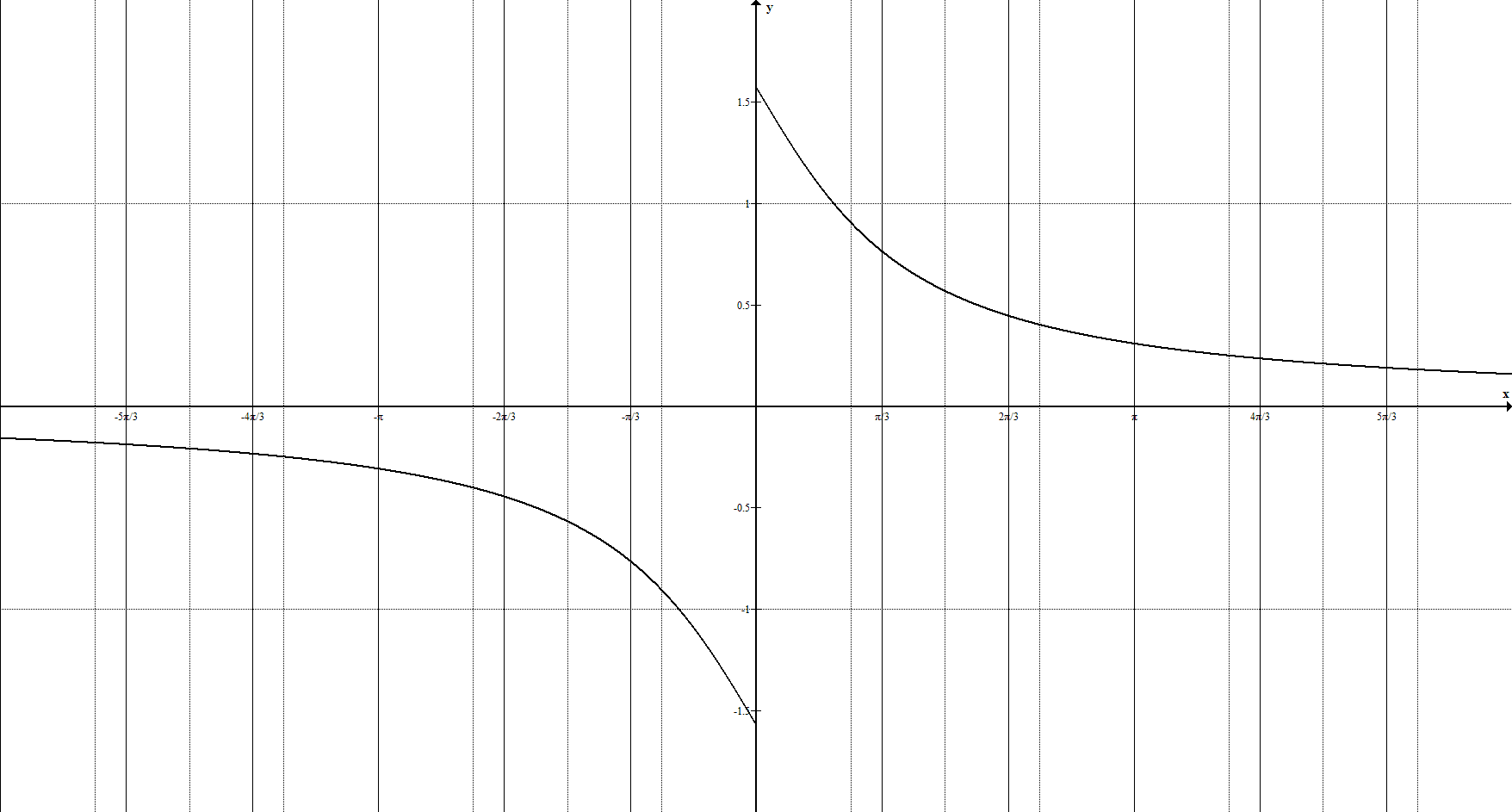
9. Обратные тригонометрические функции задаются уравнением $y=\arcsin{x}, \ y=\arccos{x}, \ y={\rm arctg}{x}, \ y={\rm arcctg}{x}$ и её график имеет вид: