Решаем неравенство с косинусом

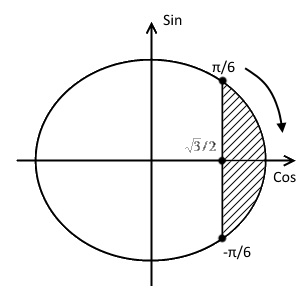
Как и с синусом, решать неравенства с косинусом мы будем с помощью единичной окружности.

Для начала рассмотрим ограничения алгоритма и частные случаи.

Ограничение алгоритма

Важно: рассматриваемый ниже алгоритм не работает для неравенств вида $\cos{x} > 1; \ \cos{x} \geq 1; \ \cos{x} < -1; \ \cos{x} \leq -1$. В строгом случае эти неравенства не имеют решений, а в нестрогом — решение сводится к решению уравнения $\cos{x} = 1$ или $\cos{x} = -1$.

Частные случаи при решении неравенства с косинусом

Важно отметить также следующие случаи, которые гораздо удобнее решить логически, не используя нижеследующий алгоритм.

Частный случай 1. Решить неравенство:

$\cos{x} \leq 1.$

Рассуждения здесь аналогичные первому частному случаю синуса. В силу того, что область значения тригонометрической функции $y=\cos{x}$ не больше по модулю $1$, то левая часть неравенства при любом $x$ из области определения (а область определения косинуса — все действительные числа) не больше $1$. А, значит, в ответ мы записываем: $x \in R$.

Следствие: аналогично решается и неравенство

$\cos{x} \geq -1.$

Частный случай 2. Решить неравенство:

$\cos{x} < 1.$

Рассуждения здесь аналогичные второму частному случаю синуса. Левая часть неравенства меньше $1$ для всех $x \in R$, кроме точек, являющихся решением уравнения $\cos{x} = 1$. Решая это уравнение, будем иметь:

$x = \pm \arccos{1} + 2 \pi n = 2 \pi n.$

А, значит, в ответ мы записываем: $x \in R \backslash 2\pi n$.

Следствие: аналогично решается и неравенство

$\cos{x} > -1.$

Алгоритм решения неравенств с косинусом:

1. на оси косинуса откладываем число $a$ и проводим прямую параллельно оси синусов до пересечения с окружностью;
2. точки пересечения будут закрашенными, если неравенство нестрогое, и не закрашенными, если неравенство строгое;
3. область будет находится справа от прямой и до окружности, если неравенство содержит знак «$>$», и слева от прямой и до окружности, если неравенство содержит знак «$<$»;
4. для нахождения точек пересечения, решаем тригонометрическое уравнение $\cos{x}=a$, получаем $x=\pm\arccos{a} + 2\pi n$;
5. полагая $n=0$, мы находим первую точку $x_{1}=\arccos{a}$ (иными словами, убираем $\pm$ и $2\pi n$ и получаем первую точку, которая находится или в первой, или во второй четверти);
6. второй точкой будет или $x_{2_{1}}=-\arccos{a}$, или $x_{2_{2}}=2\pi — \arccos{a}$. Для того, чтобы определить, какая из них будет второй точкой, смотрим, в каком направлении мы идём по области ко второй точке пересечения: если в положительном направлении, то следует брать $x_{2_{2}}$, а, если в отрицательном, то $x_{2_{1}}$;
7. в ответ выписывается промежуток от меньшей точки пересечения $+ 2\pi n$ до большей $+ 2\pi n$.

Примеры решения неравенств с помощью алгоритма.

Пример 1: Решить неравенство:

$\cos{x} \geq — \frac{1}{2}.$

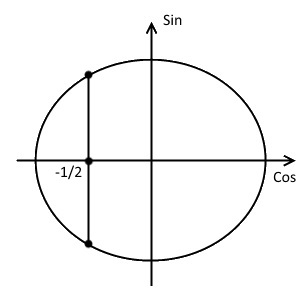
1. Отметим на оси косинусов координату $-\frac{1}{2}$.
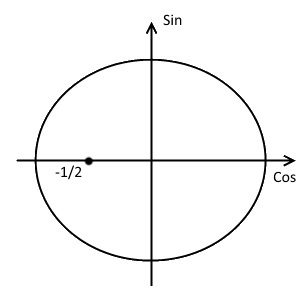
2. Проведём прямую параллельно оси синусов и проходящую через эту точку.
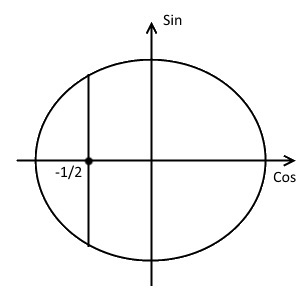
3. Отметим точки пересечения. Они будут закрашенными, так как неравенство нестрогое.
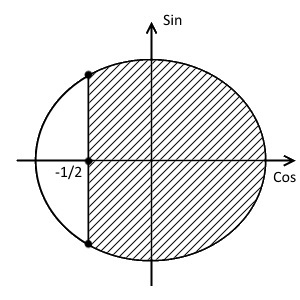
4. Знак неравенства $\geq$, а значит закрашиваем область справа от прямой, т.е. больший полукруг.
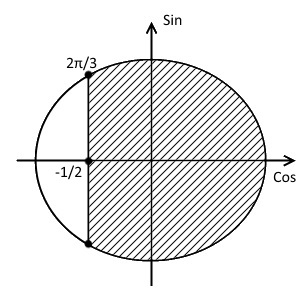
5. Находим первую точку пересечения. Для этого неравенство превращаем в равенство и решаем его: $\cos{x}=-\frac{1}{2} \ \Rightarrow \ x=\pm \arccos{\left(-\frac{1}{2}\right)}+2\pi n = \pm\frac{2\pi}{3} + 2\pi n$. Полагаем далее $n=0$ и находим первую точку пересечения: $x_{1}=\frac{2\pi}{3}$.
6. Находим вторую точку. Наша область идёт в отрицательном направлении от первой точки, значит $x_{2}=-\frac{2\pi}{3}$.

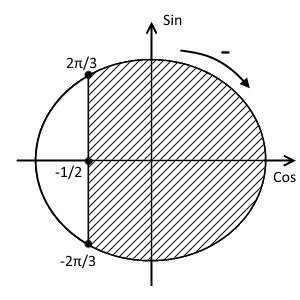
Таким образом, решение примет вид:

$x \in \left[-\frac{2\pi}{3} + 2\pi n; \frac{2\pi}{3} + 2 \pi n\right], \ n \in Z.$

Пример 2: Решить неравенство:

$\cos{x} < \frac{1}{2}$

Отметим на оси косинусов координату $\frac{1}{2}$ и проведём прямую параллельно оси синусов и проходящую через эту точку. Отметим точки пересечения. Они будут не закрашенными, так как неравенство строгое. Знак неравенства $<$, а, значит, закрашиваем область слева от прямой, т.е. больший полукруг. Неравенство превращаем в равенство и решаем его:

$\cos{x}=\frac{1}{2}$

$x=\pm\arccos{\frac{1}{2}}+ 2\pi n = \pm\frac{\pi}{3} + 2\pi n.$

Итак, первая точка пересечения: $x_{1}=\frac{\pi}{3}$. Наша область идёт в положительном направлении от первой точки, значит: $x_{2}= 2\pi — \frac{\pi}{3} = \frac{5\pi}{3}$.

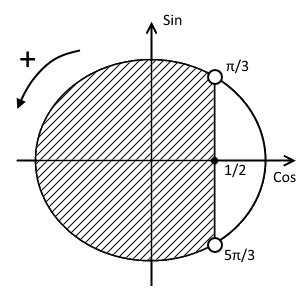Итак, решением этого неравенства будет промежуток:

$x \in \left(\frac{\pi}{3} + 2\pi n; \frac{5\pi}{3} + 2 \pi n\right), \ n \in Z.$

Пример 3: Решить неравенство:

$2\cos{\left(2x-\frac{\pi}{6}\right)} — \sqrt{3} \geq 0.$

Сейчас применить алгоритм нельзя. Этот пример похож на пример 3 неравенства с синусом. И действовать нужно аналогично. Сначала перенесём всё, что не содержит тригонометрической функции в правую часть.

$2\cos{\left(2x-\frac{\pi}{6}\right)} \geq \sqrt{3}.$

Разделим на коэффициент при тригонометрической функции, если он не равен $1$ (не забываем про знак!).

$\cos{\left(2x-\frac{\pi}{6}\right)} \geq \frac{\sqrt{3}}{2}.$

Теперь же, чтобы применить алгоритм, делаем замену переменной. Всё, что стоит под тригонометрической функцией, обозначаем за новую переменную:

$t=2x-\frac{\pi}{6}$

и получаем неравенство

$\cos{t} \geq \frac{\sqrt{3}}{2},$

которое мы можем решить с помощью алгоритма.

Итак, получено:

$t \in \left[-\frac{\pi}{6}+2\pi n;\frac{\pi}{6}+2\pi n\right]$

Возвращаемся к исходной переменной:

$\left(2x-\frac{\pi}{6}\right) \in \left[-\frac{\pi}{6}+2\pi n;\frac{\pi}{6}+2\pi n\right].$

Последнее равносильно системе неравенств

$\left\{\begin{array}{c} 2x-\frac{\pi}{6} \geq -\frac{\pi}{6}+2\pi n, \\ 2x-\frac{\pi}{6} \leq \frac{\pi}{6}+2\pi n, \end{array} \right.$

решив которую мы получим ответ. Действительно,

$\left\{\begin{array}{c} 2x \geq \frac{\pi}{6}-\frac{\pi}{6}+2\pi n, \\ 2x \leq \frac{\pi}{6}+\frac{\pi}{6}+2\pi n, \end{array} \right.$

$\left\{\begin{array}{c} 2x \geq 2\pi n, \\ 2x \leq \frac{\pi}{3}+2\pi n, \end{array} \right. $

$\left\{\begin{array}{c} x \geq \pi n, \\ x \leq \frac{\pi}{6}+\pi n. \end{array} \right. $

И окончательно получаем:

$x \in \left[\pi n; \frac{\pi}{6} + \pi n\right], \ n \in Z.$