Перед вами четвёртая статья из цикла «Геометрические преобразования графиков функций«.
1. Отображение относительно оси $Ox$.
Важно:
Данное преобразование имеет место тогда и только тогда, когда $k_{2}<0$.
Правило:
Чтобы построить график функции $y=-f(x)$, необходимо каждую точку графика функции $y=f(x)$ симметрично отобразить относительно оси $Ox$.
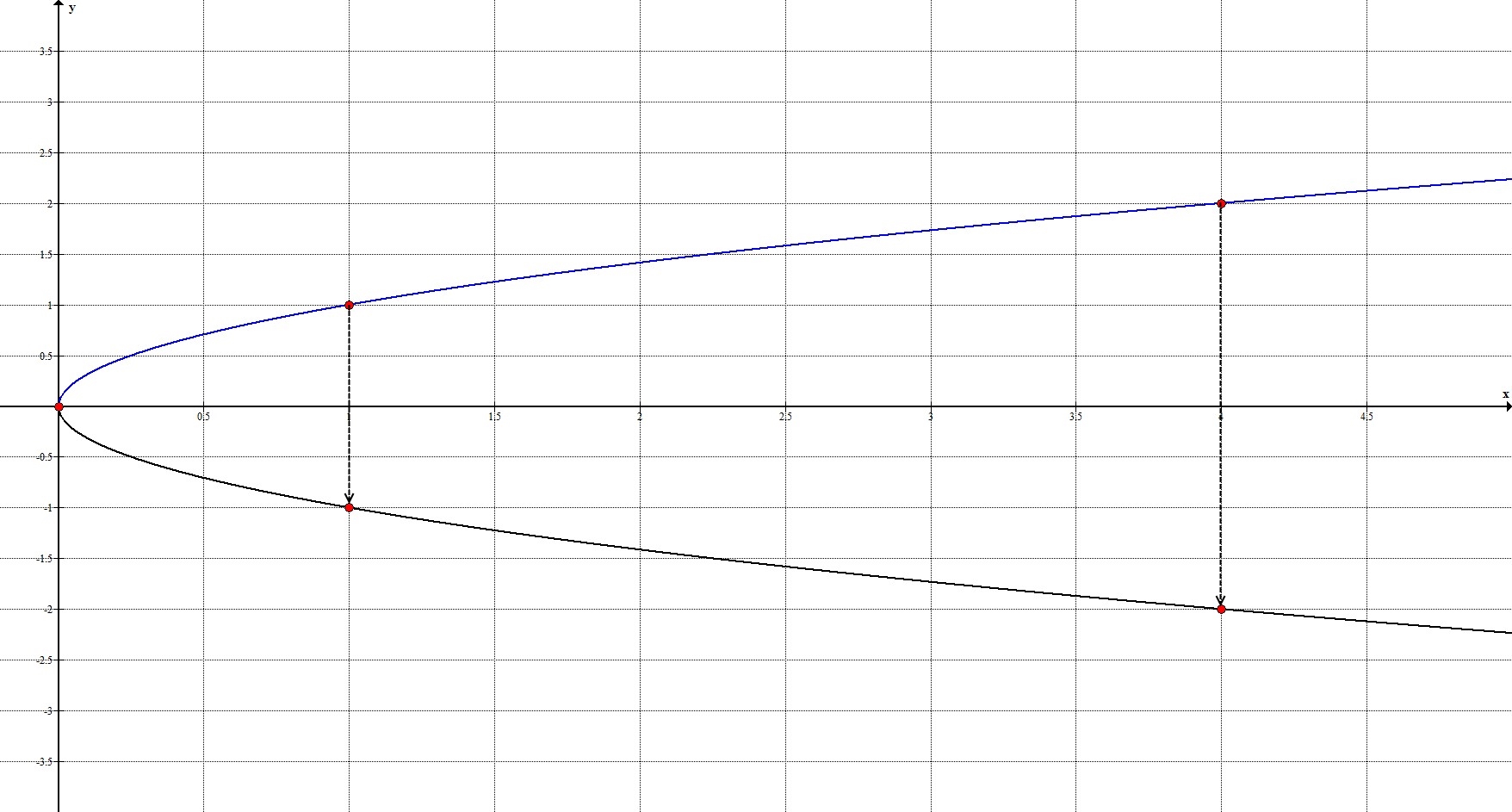
Рассмотрим это преобразование на примере: $y=-\sqrt{x}$
Прообразом этой функции будет $y_0=\sqrt{x}$.
$k_2=-1 < 0 \Rightarrow$ происходит отображение относительно оси $Ox$.
Рассмотрим ключевые точки функции: $(0;0), \ (1;1), \ (4;2)$.
Не изменяя координату $x$, в каждой ключевой точке поставим в координате $y$ противоположный знак (был «-«, а станет «+», и наоборот), то есть:
$(0;0) \rightarrow x=0; y=-0=0 \rightarrow (0;0)$;
$(1;1) \rightarrow x=1; y=-1 \rightarrow (1;-1)$;
$(4;2) \rightarrow x=4; y=-2 \rightarrow (4;-2)$.
То есть, наши ключевые точки переходят в точки $(0;0), \ (1;-1), \ (4;-2)$.
2. Отображение относительно оси $Oy$.
Важно:
Данное преобразование имеет место тогда и только тогда, когда $k_{1}<0$.
Правило:
Чтобы построить график функции $y=f(-x)$, необходимо каждую точку графика функции $y=f(x)$ симметрично отобразить относительно оси $Oy$.
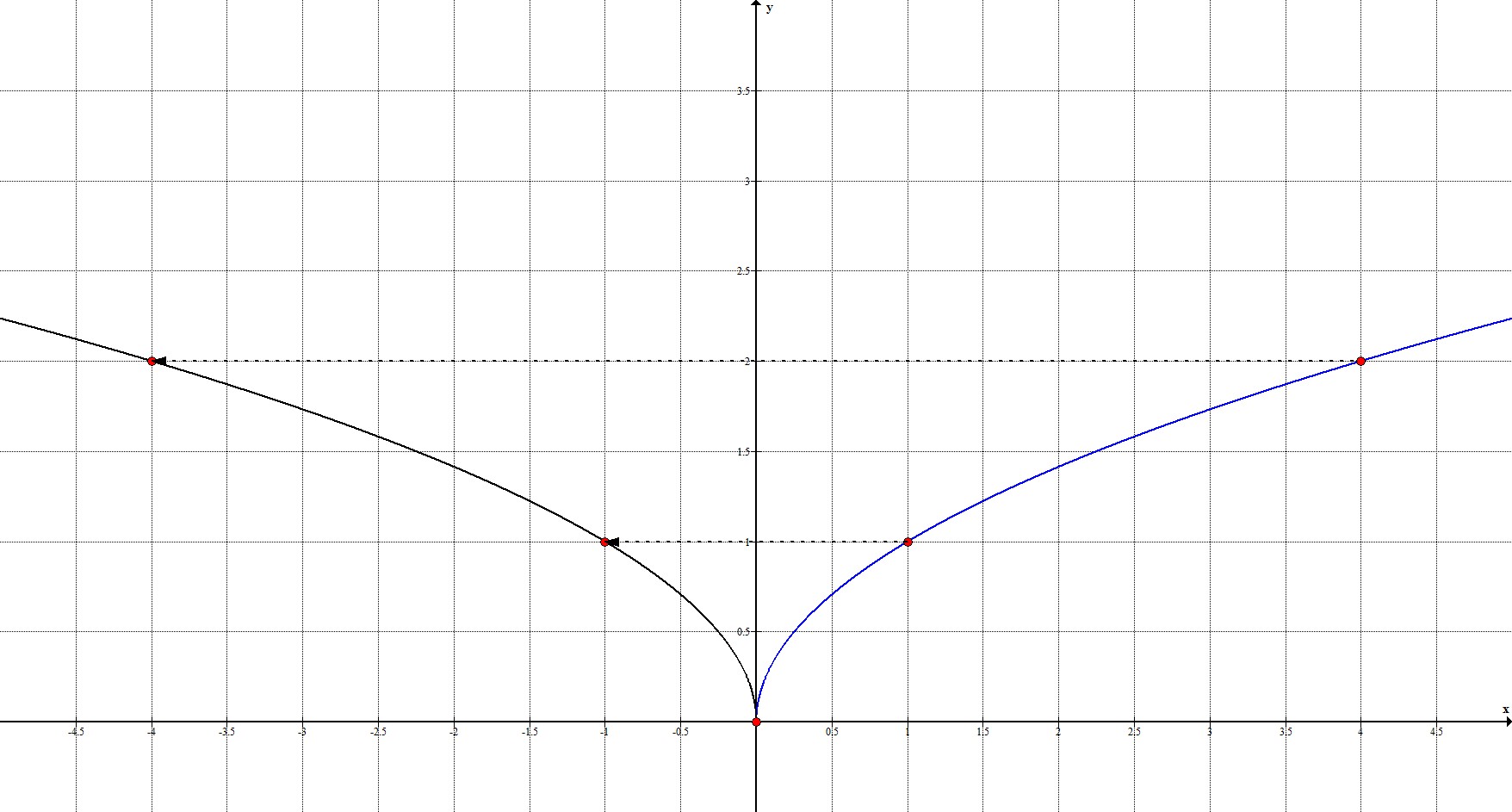
Рассмотрим это преобразование на примере: $y=\sqrt{-x}$
Прообразом этой функции будет $y_0=\sqrt{x}$.
$k_1=-1 < 0 \Rightarrow$ происходит отображение относительно оси $Oy$.
Рассмотрим ключевые точки функции: $(0;0), \ (1;1), \ (4;2)$.
Не изменяя координату $y$, в каждой ключевой точке поставим в координате $x$ противоположный знак (был «-«, а станет «+», и наоборот), то есть:
$(0;0) \rightarrow x=-0=0; y=0 \rightarrow (0;0)$;
$(1;1) \rightarrow x=-1; y=1 \rightarrow (-1;1)$;
$(4;2) \rightarrow x=-4; y=2 \rightarrow (-4;2)$.
То есть, наши ключевые точки переходят в точки $(0;0), \ (-1;1), \ (-4;2)$.