Понятие о логарифме.
При решении показательных уравнений, мы старались привести показательные функции к одному основанию. А что делать, если, например, правая часть не представима в виде степени с основанием, стоящим в левой части? Например, как решить уравнение $2^{x}=5$? Ведь $5$ не представима в виде степени $2$-ки! Тут на помощь приходит логарифм.
Пусть $a>0$, $a \neq 1$ и $b>0$.
Определение 1: Логарифмом числа $b$ по основанию $a$ называется показатель степени, в которую нужно возвести число $a$, чтобы получить число $b$.
Определение 2: Число, выражение или функция $b$ называется подлогарифмическим числом, выражением или функцией.
Логарифм числа $b$ по основанию $a$ обозначается $\log_{a}{b}$ и читается: »логарифм числа $b$ по основанию $a$» или иногда: »логарифм $b$ по $a$».
Согласно определению, $\log_{2}{4}=2$, так как $2^{2}=4$. Ответом на наш загадочный пример $2^{x}=5$ будет $x=\log\limits_{2}{5}$.
Наглядно определение может выглядеть как показано на следующем рисунке:
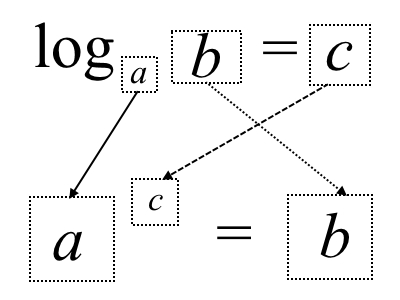
Из определения сразу следует следующая теорема.
Теорема (Основное свойство логарифма): Если $b>0$, $a>0$, $a \neq 1$, то
$a^{\log_{a}{b}} = b$
Основные свойства логарифмов.
При решении задач на практике иногда требуется формула перехода из одного основания к другому. Например, такой логарифм: $\log_{4}{2}$ проще найти, если перейти от основания $4$ к основанию $2$.
Формула перехода от основания $a$ к основанию $b$: Пусть $a>0, \ a \neq 1, \ b>0, \ b \neq 1$ и $x>0$, тогда формула перехода от основания $a$ к основанию $b$ примет вид:
$\log_{a}{x} = \frac{\log_{b}{x}}{\log_{b}{a}}.$
Таким образом,
$\log_{4}{2}=\frac{\log_{2}{2}}{\log_{2}{4}}=\frac{1}{2}.$
Для любого $a>0, \ a \neq 1$, любых положительных $x$ и $y$ и любого действительного $p$ справедливы формулы:
Первое свойство:
$\log_{a}{1} = 0$.
Воспользуемся определением логарифма:
$a^{0} = 1 \equiv 1.$
Второе свойство:
$\log_{a}{a} = 1$.
Воспользуемся определением логарифма:
$a^{1} = a \equiv a.$
Третье свойство:
$\log_{a}{x \cdot y} = \log_{a}{x} + \log_{a}{y}$.
По основному логарифмическому свойству,
$x = a^{\log_{a}{x}}, \ y = a^{\log_{a}{y}}.$
$x \cdot y = a^{\log_{a}{x}} \cdot a^{\log_{a}{y}} = a^{\log_{a}{x} + \log_{a}{y}}.$
Возьмём логарифм по основанию $a$ от левой и правой части, получим:
$\log_{a}{x \cdot y} = \log_{a}{a^{\log_{a}{x} + \log_{a}{y}}} = \log_{a}{x} + \log_{a}{y}.$
Четвёртое свойство:
$\log_{a}{\frac{x}{y}} = \log_{a}{x} — \log_{a}{y}$.
$\log_{a}{\frac{x}{y}} = \log_{a}{x \cdot y^{-1}} = $
По третьему свойству, получим:
$= \log_{a}{x} + \log_{a}{y^{-1}} = $
По пятому свойству, будем иметь:
$=\log_{a}{x} + (-1) \cdot \log_{a}{y} = \log_{a}{x} — \log_{a}{y}.$
Пятое свойство:
$\log_{a}{x^{p}} = p \cdot \log_{a}{x}$.
Используя основное логарифмическое свойство перепишем $x$ в виде
$x = a^{\log_{a}{x}}.$
Возведём левую и правую часть в степень $p$.
$x^{p} = \left(a^{\log_{a}{x}}\right)^{p} = a^{p \cdot \log_{a}{x}}.$
Возьмём логарифм по основанию $a$ от левой и правой части, получим:
$\log_{a}{x^{p}} = \log_{a}{a^{p \cdot \log_{a}{x}}} = p \cdot \log_{a}{x}.$
Шестое свойство:
$\log_{a^{p}}{x} = \frac{1}{p} \cdot \log_{a}{x}$.
Перейдём от основания $a^{p}$ к основанию $a$ с помощью формулы перехода.
$\log_{a^{p}}{x} = \frac{\log_{a}{x}}{\log_{a}{a^{p}}} =$
По пятому свойству, получим:
$= \frac{\log_{a}{x}}{p \cdot \log_{a}{a}} = $
По второму свойству, будем иметь:
$= \frac{\log\limits_{a}{x}}{p}.$
