Перед вами вторая статья из цикла «Геометрические преобразования графиков функций«.
1. Параллельный перенос по оси $Ox$ на $|a|$ единиц.
Правило:
Чтобы построить график функции $y=f(x + a)$, необходимо каждую точку графика функции $y=f(x)$ сместить влево (если $a>0$) или вправо (если $a<0$) по оси $Ox$ на $|a|$ единиц.
Рассмотрим это преобразование на примерах.
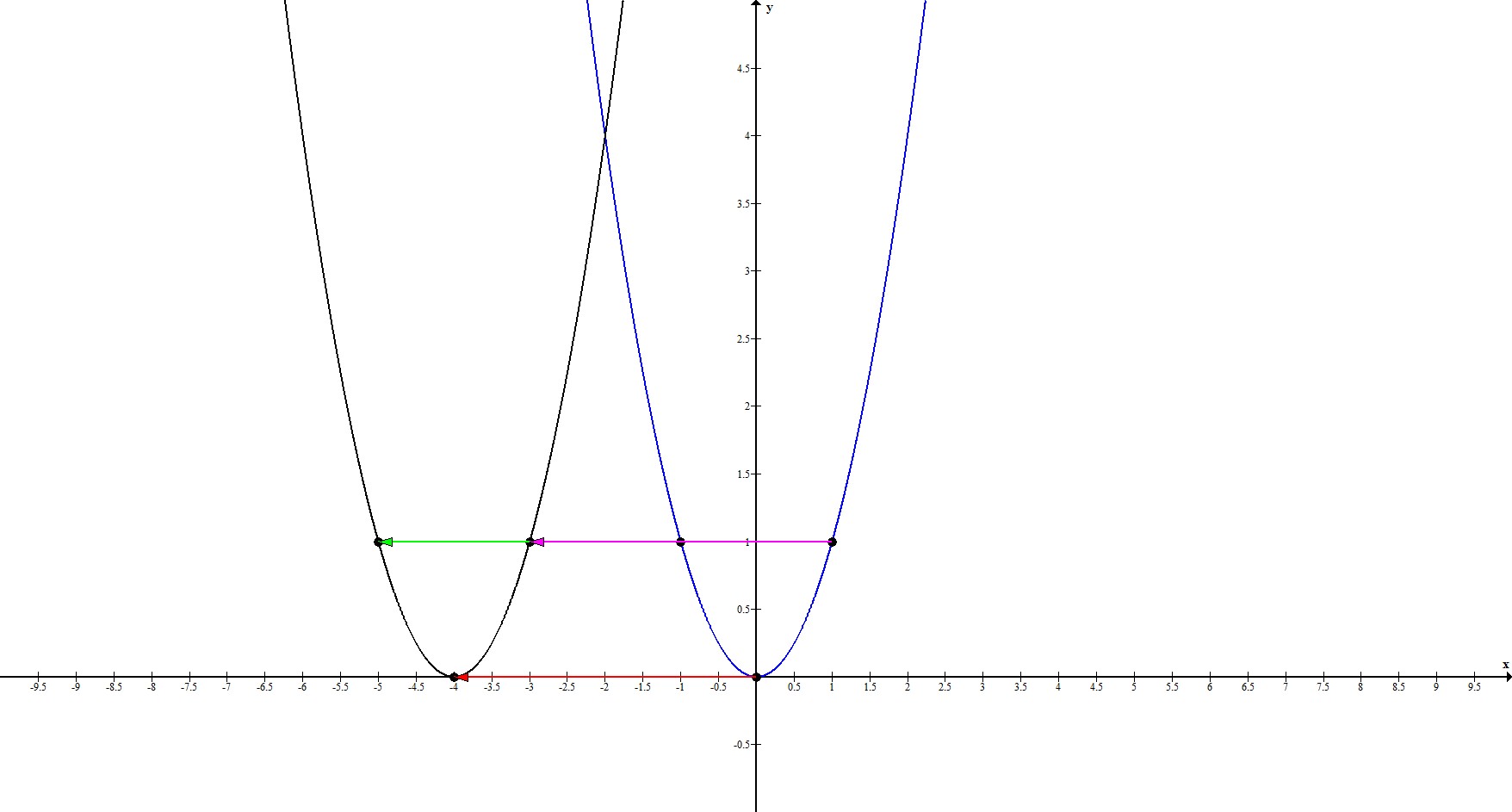
1. $y=(x+4)^2$
Прообразом этой функции будет $y_0=x^2$.
$a=4>0 \Rightarrow$ происходит параллельный перенос на $4$ единицы влево.
Рассмотрим ключевые точки функции: $(-1;1), \ (0;0), \ (1;1)$. Координата по $x$ каждой точки смещается на 4 влево. То есть, наши ключевые точки переходят в точки $(-5;1), \ (-4;0), \ (-3;1)$.
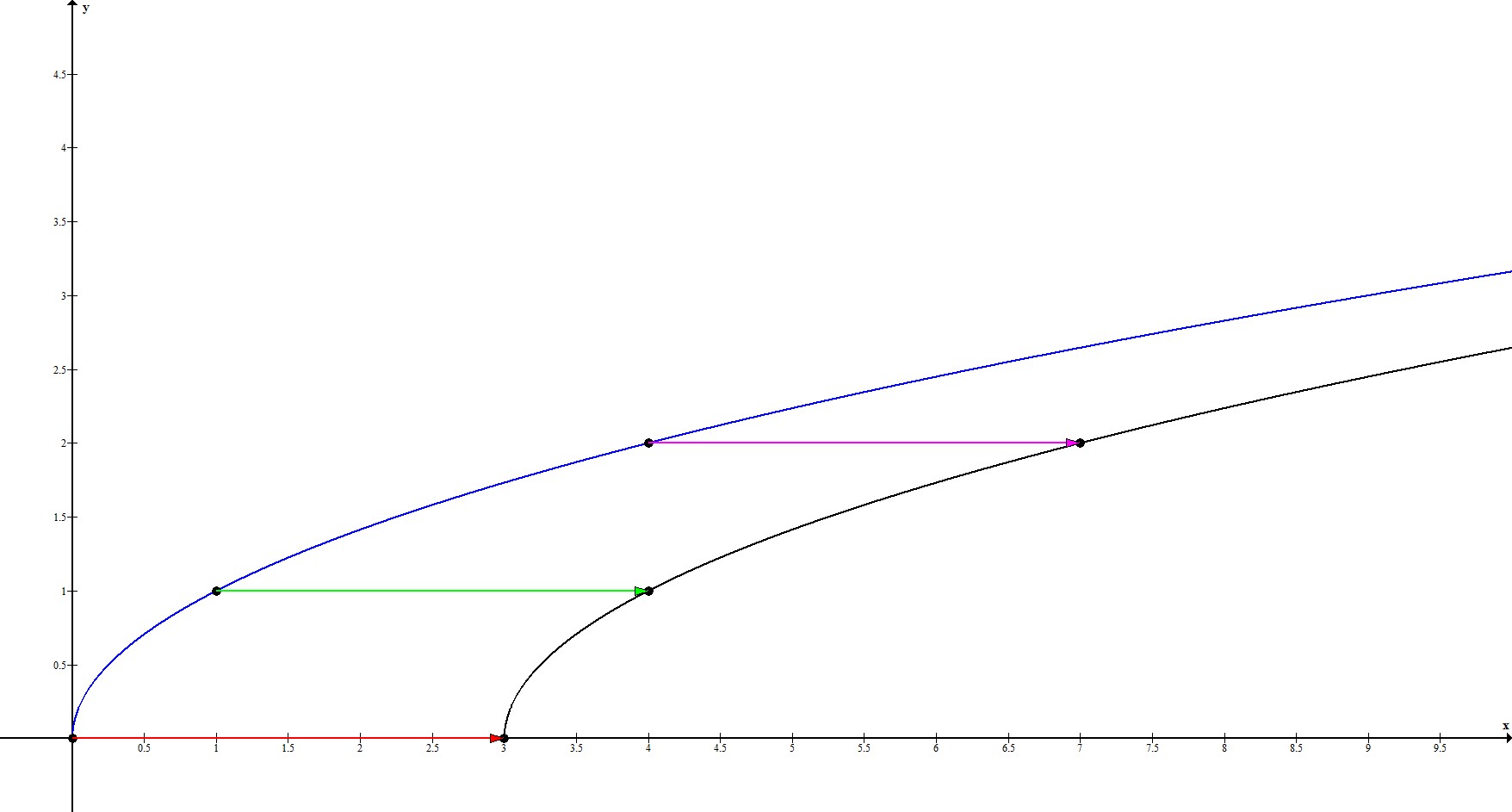
2. $y=\sqrt{x-3}$
Прообразом этой функции будет $y_0=\sqrt{x}$.
$a=-3<0 \Rightarrow$ происходит параллельный перенос на $3$ единицы вправо.
Рассмотрим ключевые точки функции: $(0;0), \ (1;1), \ (4;2)$. Координата по $x$ каждой точки смещается на 3 вправо. То есть, наши ключевые точки переходят в точки $(3;0), \ (4;1), \ (7;2)$.
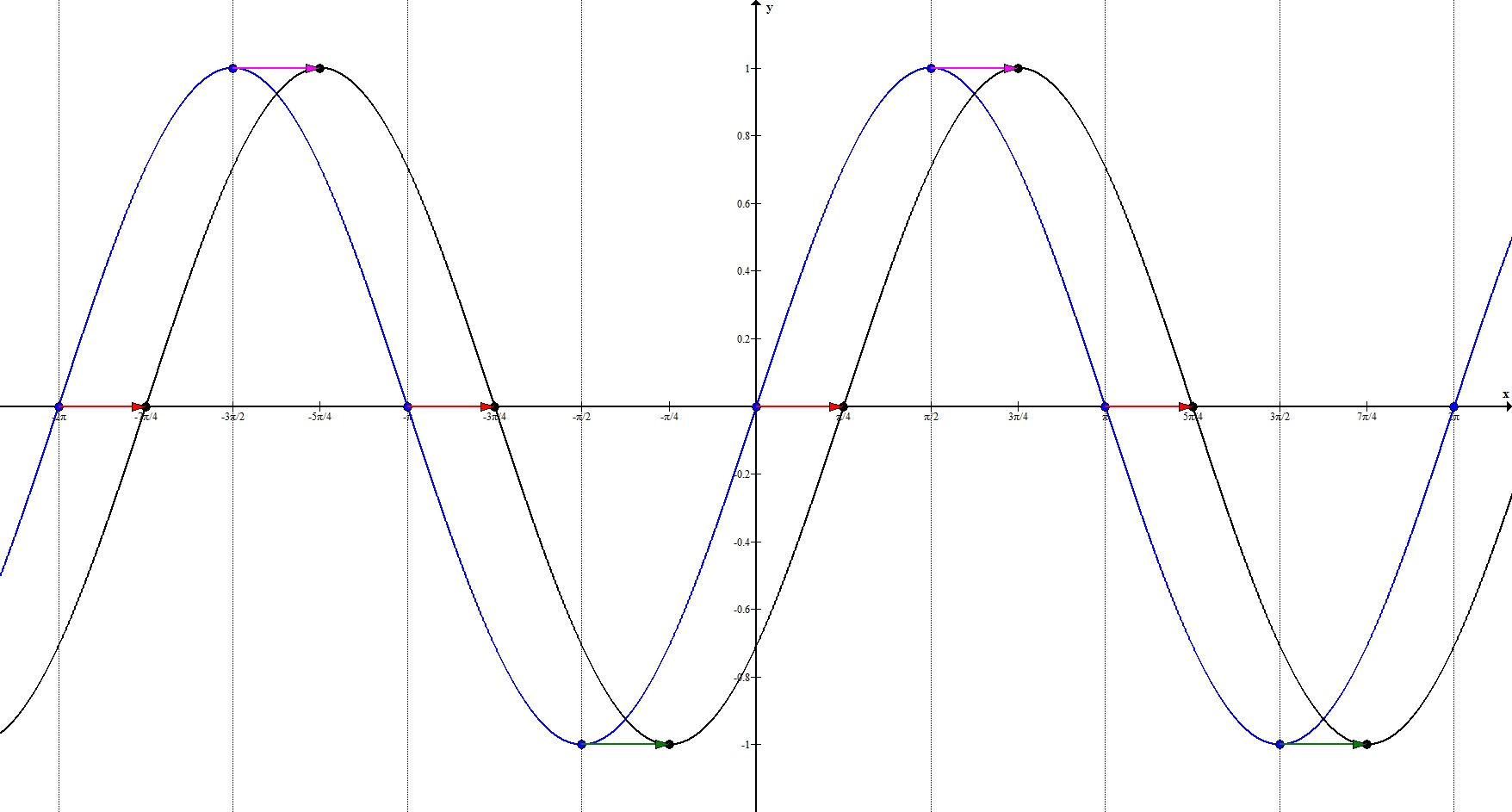
3. $y=\sin{x-\frac{\pi}{4}}$
Прообразом этой функции будет $y_0=\sin{x}$.
$a=-\frac{\pi}{4}<0 \Rightarrow$ происходит параллельный перенос на $\frac{\pi}{4}$ единицы вправо.
Рассмотрим ключевые точки функции:
$(-2\pi; 0), \ \left(-\frac{3\pi}{2}; 1\right), \ (-\pi;0), \left(-\frac{\pi}{2}; -1\right), \ (0;0), \ \left(\frac{\pi}{2}; 1\right), \ (\pi; 0), \ \left(\frac{3\pi}{2}; -1\right), \ (2\pi; 0)$
Координата по $x$ каждой точки смещается на $\frac{\pi}{4}$ вправо. То есть, наши ключевые точки переходят в точки
$(-\frac{7\pi}{4}; 0), \ \left(-\frac{5\pi}{4}; 1\right), \ \left(-\frac{3\pi}{4};0\right), \left(-\frac{\pi}{4}; -1\right), \ \left(\frac{\pi}{4};0\right), \ \left(\frac{3\pi}{4}; 1\right), \ \left(\frac{5\pi}{4}; 0\right), \ \left(\frac{7\pi}{4}; -1\right), \ \left(\frac{9\pi}{4}; 0\right)$.
2. Параллельный перенос по оси $Oy$ на $|b|$ единиц.
Правило:
Чтобы построить график функции $y=f(x) + b$, необходимо каждую точку графика функции $y=f(x)$ поднять вверх (если$b>0$) или опустить вниз (если $b<0$) по оси $Oy$ на $|b|$ единиц.
Рассмотрим это преобразование на примерах.
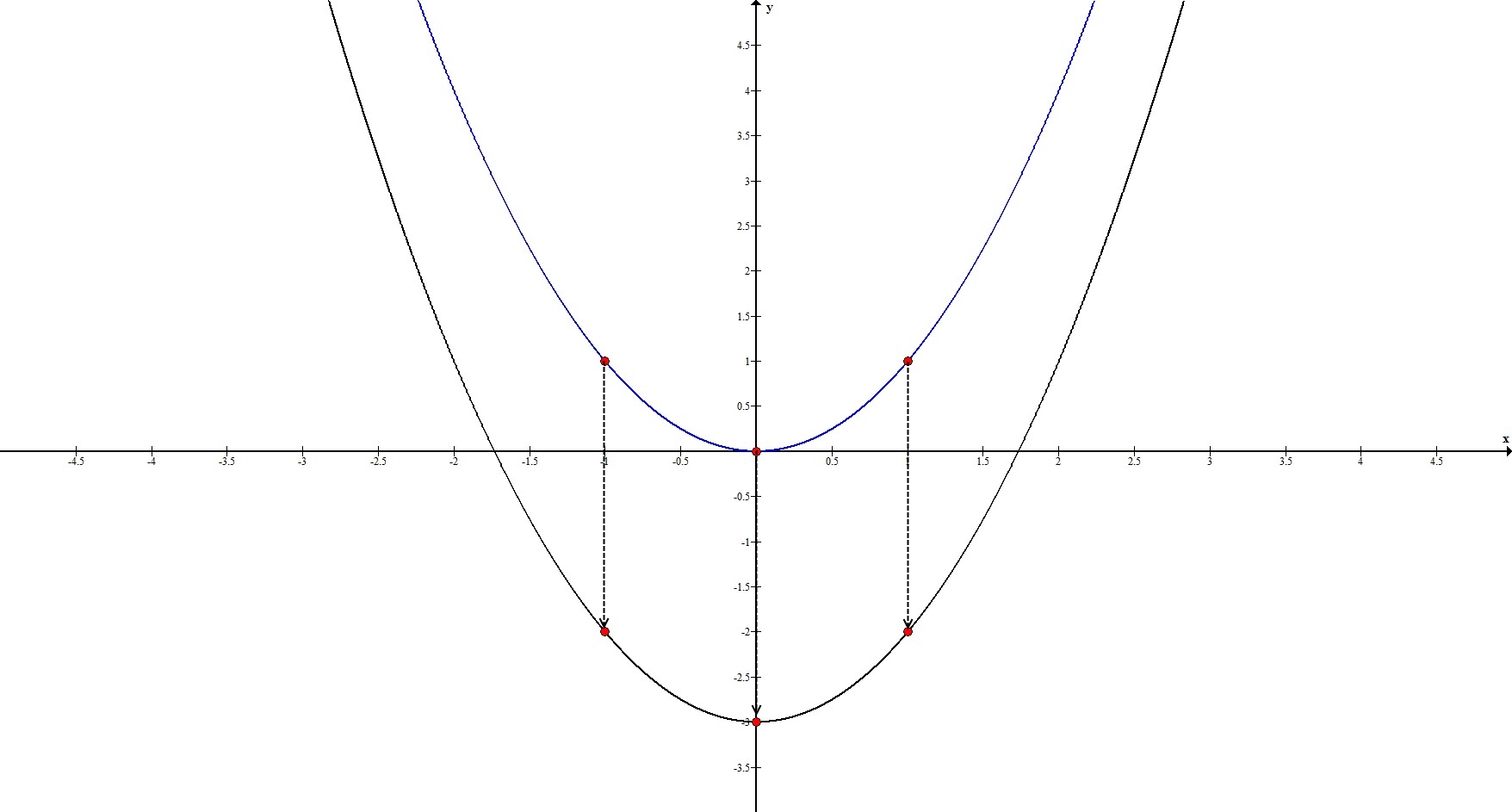
1. $y=x^2-3$
Прообразом этой функции будет $y_0=x^2$.
$b=-3<0 \Rightarrow$ происходит параллельный перенос на $3$ единицы вниз.
Рассмотрим ключевые точки функции: $(-1;1), \ (0;0), \ (1;1)$. Координата по $y$ каждой точки смещается на 3 вниз. То есть, наши ключевые точки переходят в точки $(-1;-2), \ (0;-3), \ (1;-2)$.
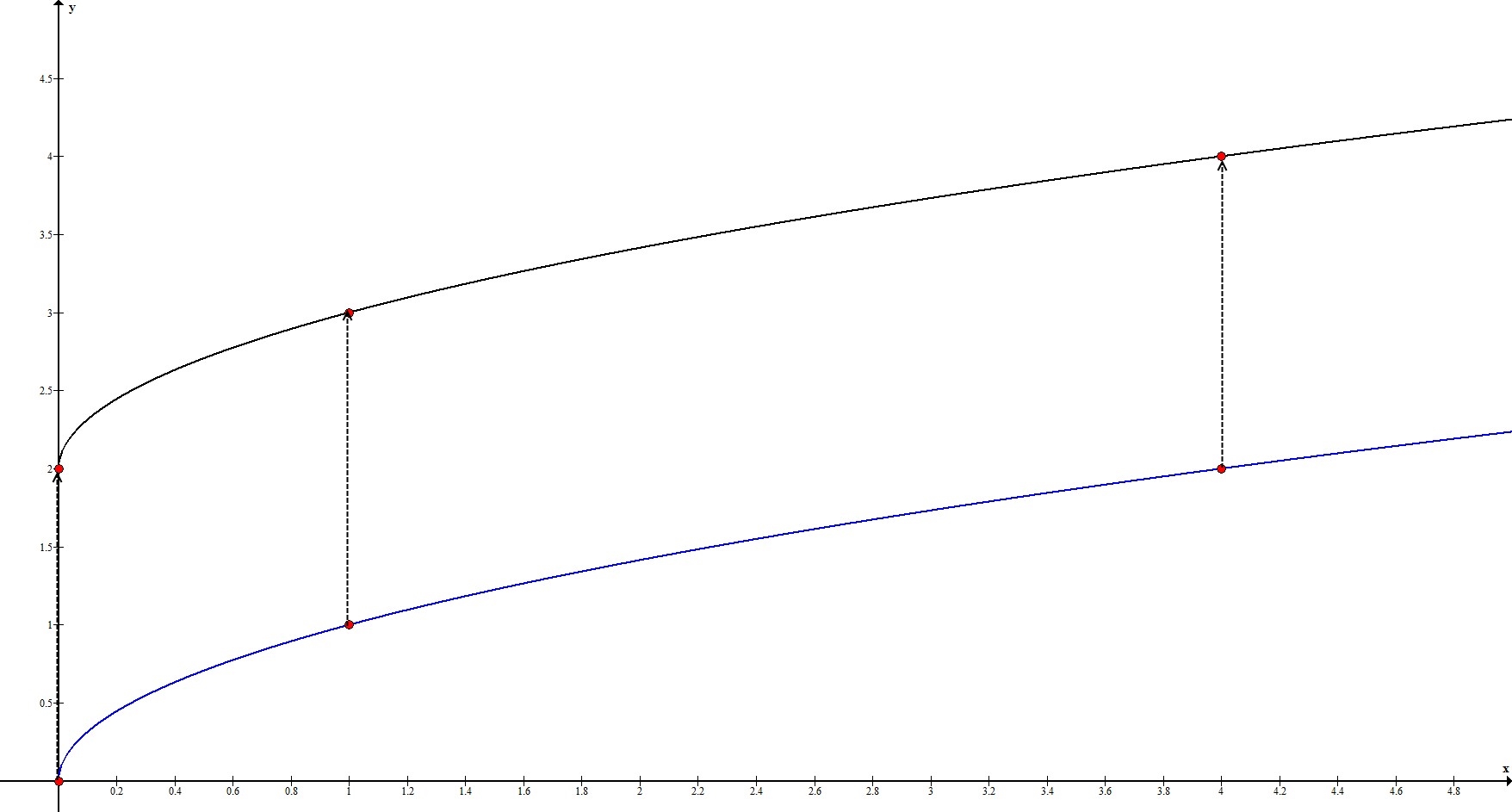
2. $y=\sqrt{x}+2$
Прообразом этой функции будет $y_0=\sqrt{x}$.
$b=2>0 \Rightarrow$ происходит параллельный перенос на $2$ единицы вверх.
Рассмотрим ключевые точки функции: $(0;0), \ (1;1), \ (4;2)$. Координата по $y$ каждой точки смещается на 2 вверх. То есть, наши ключевые точки переходят в точки $(0;2), \ (1;3), \ (4;4)$.
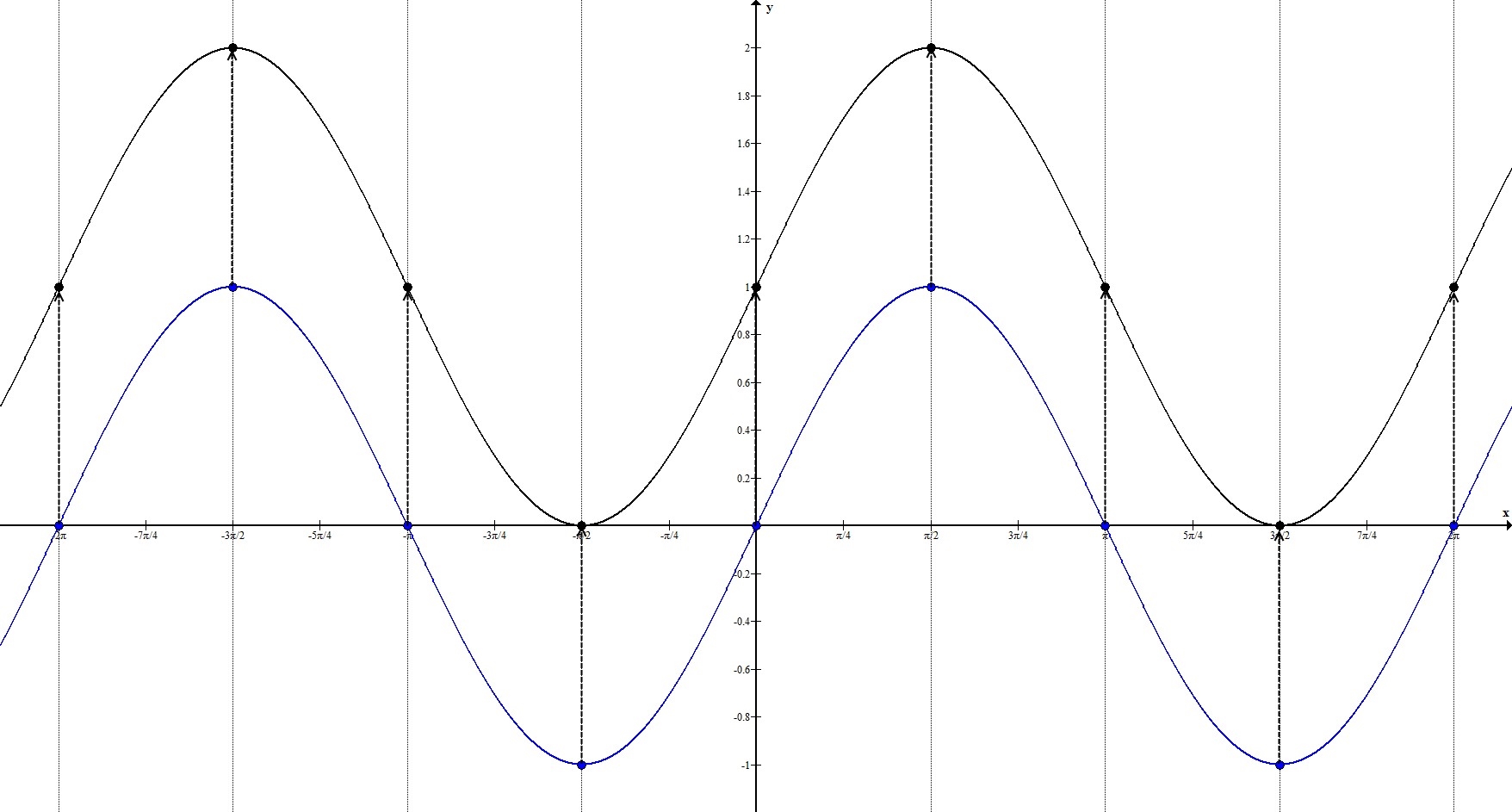
3. $y=\sin{x}+1$
Прообразом этой функции будет $y_0=\sin{x}$.
$b=1>0 \Rightarrow$ происходит параллельный перенос на 1 единицу вверх.
Рассмотрим ключевые точки функции:
$(-2\pi; 0), \ \left(-\frac{3\pi}{2}; 1\right), \ (-\pi;0), \left(-\frac{\pi}{2}; -1\right), \ (0;0), \ \left(\frac{\pi}{2}; 1\right), \ (\pi; 0), \ \left(\frac{3\pi}{2}; -1\right), \ (2\pi; 0)$
Координата по $y$ каждой точки смещается на 1 вверх. То есть, наши ключевые точки переходят в точки
$(-2\pi; 1), \ \left(-\frac{3\pi}{2}; 2\right), \ (-\pi;1), \left(-\frac{\pi}{2}; 0\right), \ (0;1), \ \left(\frac{\pi}{2}; 2\right), \ (\pi; 1), \ \left(\frac{3\pi}{2}; 0\right), \ (2\pi; 1)$.