Аксиомы планиметрии
Система аксиом планиметрии состоит из девяти аксиом (ПI — ПIX). Сформулируем каждую из них.
Аксиома ПI. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую и притом только одну.
Аксиома ПII. Из трёх точек на прямой одна и только одна лежит между двумя другими.
Аксиома ПIII. Каждый отрезок имеет определённую длину, большую нуля. Причём, если отрезок разбить конечным числом точек, то его длина будет равняться сумме длин частей, на которые он разбивается этими точками.
Аксиома ПIV. Прямая, принадлежащая плоскости, разбивает эту плоскость на две полуплоскости.
Аксиома ПV. Каждый угол имеет определённую меру, большую нуля. Развёрнутый угол в градусной мере равен 180°. Мера угла равна сумме мер углов, на которые он разбивается конечным числом лучей, проходящих между его сторонами.
Аксиома ПVI. На любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и притом только один.
Аксиома ПVII. От полупрямой на содержащей её плоскости в заданную полуплоскость можно отложить угол с заданной мерой, меньшей меры развёрнутого угла, и притом только один.
Аксиома ПVIII. Каков бы ни был треугольник, существует равный ему в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.
Аксиома ПIX. На плоскости через данную точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну.
Основными фигурами планиметрии являются точка и прямая. На их основе строятся все фигуры планиметрии.
Треугольники
Определение: Треугольником называется фигура, состоящая из трёх точек, не лежащих на одной прямой и называемых вершинами, и трёх отрезков, попарно соединяющих эти точки и называемых сторонами.
Классификация треугольников
Треугольники делятся по:
I. Сторонам:
→ Разносторонние — треугольники, у которых все стороны разные.
→Равнобедренные — треугольники, у которых две стороны равны. Равные стороны называются боковыми сторонами, а оставшаяся сторона — основанием. Равные углы между боковыми сторонами и основанием называются боковыми углами. Высота, проведённая из вершины к основанию является медианой и биссектрисой.
→Равносторонние (или правильные) — треугольники, у которых все стороны равны. Равносторонний треугольник будет равнобедренным для любой своей стороны. Углы равны $60^{\circ}$. Справедливы формулы для радиусов описанной ($R$) и вписанной ($r$) окружностей при известной стороне ($a$):
$R = \frac{\sqrt{3}}{3} \cdot a; \ r = \frac{\sqrt{3}}{6} \cdot a; \ R = 2 \cdot r.$
II. Углам:
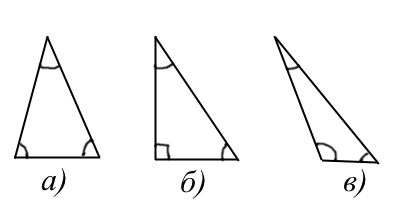
→Остроугольные — треугольники, у которых все углы меньше $90^{\circ}$.
→Прямоугольные — треугольники, у которых один угол равен $90^{\circ}$. Стороны, прилежащие к прямому углу называются катетами, а оставшаяся сторона — гипотенузой. Справедлива теорема Пифагора.
→Тупоугольные — треугольники, у которых один угол больше $90^{\circ}$.
Определение: Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны.
Признаки равенства треугольников
Первый признак: Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Второй признак: Если сторона и два прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак: Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
Определение: Треугольники называются подобными, если у них углы соответственно равны, а стороны одного пропорциональны соответствующим сторонам другого треугольника.
Признаки подобия треугольников
Первый признак: Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.
Второй признак: Если угол одного треугольника равен углу другого треугольника, а стороны, образующие этот угол, пропорциональны в равном отношении, то такие треугольники подобны.
Третий признак: Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого, то такие треугольники подобны.
Определение: Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противоположную сторону.
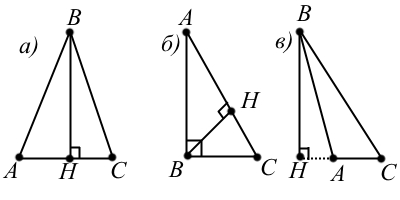
Основные свойства высоты:
- Высоты треугольника пересекаются в одной точке, называемой ортоцентром.
- Высота прямоугольного треугольника, опущенная из прямого угла, разбивает треугольник на два подобных исходному.
- Две высоты остроугольного треугольника отсекают от него подобные треугольники.
Определение: Медианой треугольника называют отрезок, соединяющий вершину треугольника со серединой противоположной стороны.
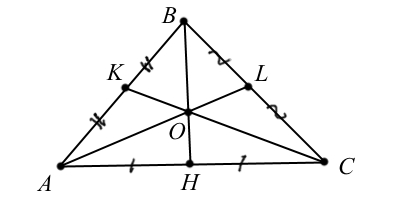
Основные свойства медианы:
- Медианы треугольника пересекаются в одной точке $O$, называемой центроидом.
- $AO:OL = BO:OH = CO:OK = 2:1$.
- Большей стороне треугольника соответствует меньшая медиана.
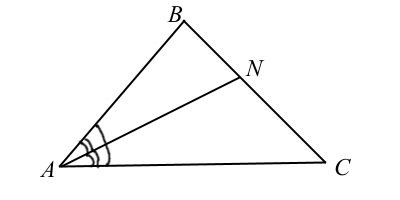
Определение: Биссектрисой треугольника называют отрезок, выходящий из вершины к противоположной стороне и делящий угол при вершине на равные углы.
Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
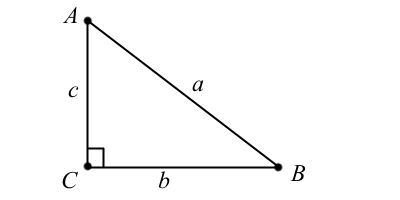
Согласно рисунку,
$a^{2} = b^{2} + c^{2}.$
Далее мы будем использовать обозначения, изображённые на рисунке:
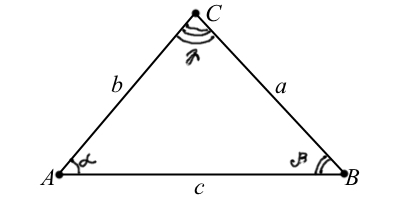
Теорема о сумме углов треугольника: Сумма всех углов треугольника равна $180^{\circ}$, т.е.
$\alpha + \beta + \gamma = 180^{\circ}.$
Теорема синусов:
$\frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma} = 2R.$
Теорема косинусов:
$c^2 = a^2 + b^2 — 2ab \cdot \cos \gamma.$
Четырёхугольники
Определение: Четырёхугольником называется фигура, которая состоит из четырёх точек и четырёх последовательно их соединяющих отрезков.
Параллелограмм
Определение: Параллелограммом называется четырёхугольник, у которого противолежащие стороны параллельны.
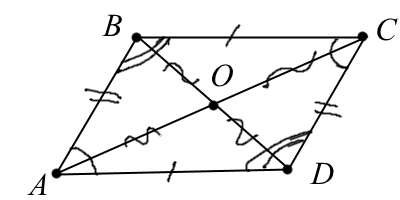
Теоремы:
1. Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм.
2. У параллелограмма противолежащие стороны и противоположные углы равны.
Прямоугольник
Определение: Прямоугольником называется параллелограмм, у которого все углы прямые.
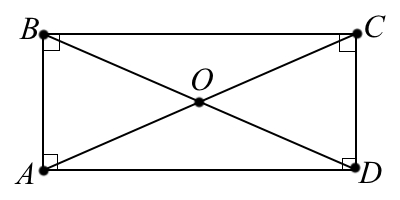
Теорема: Диагонали прямоугольника равны.
Ромб
Определение: Ромбом называется параллелограмм, у которого все стороны равны.
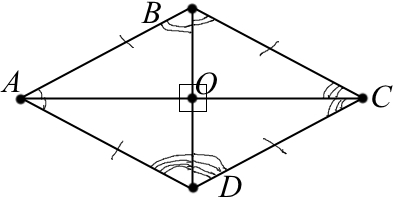
Теорема: Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
Квадрат
Определение: Квадратом (или правильным четырёхугольником) называется прямоугольник, у которого все стороны равны.
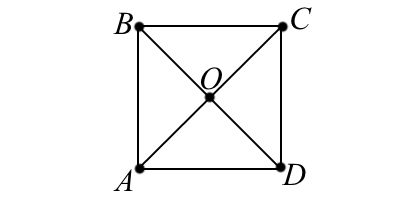
Свойства квадрата:
- У квадрата все углы прямые.
- Диагонали квадрата равны.
- Диагонали квадрата пересекаются под прямым углом и являются биссектрисами его углов.
Периметр и площадь
Мы будем использовать далее следующие обозначения: $a_{i}$ — сторона, $h_{a_{i}}$ — высота, опущенная на сторону $a_{i}$, $p=\frac{P}{2}$ — полупериметр.
Периметр
Справедливы формулы:
- Периметр треугольника: $P = a_{1} + a_{2} + a_{3}.$
- Периметр параллелограмма и прямоугольника: $P = 2 \cdot \left(a_{1} + a_{2}\right).$
- Периметр ромба и квадрата: $P = 4 \cdot a.$
Площадь
Справедливы формулы:
Площадь треугольника:
1. По стороне и высоте к ней:
$S = \frac{1}{2} \cdot a \cdot h_{a}.$
2. По двум сторонам и углу между ними:
$S = \frac{1}{2} \cdot a_{1} \cdot a_{2} \cdot \sin{\angle\widehat{a_{1},a_{2}}}.$
3. По трём сторонам (ф. Герона):
$S = \sqrt{p\left(p-a_{1}\right))\left(p-a_{2}\right)\left(p-a_{3}\right)}.$
Площадь параллелограмма:
$S=a \cdot h_{a}.$
Площадь прямоугольника:
$S=a_{1} \cdot a_{2}.$
Площадь квадрата:
$S=a^{2}.$
Площадь правильного шестиугольника:
$S = \frac{3 \cdot \sqrt{3}}{2} \cdot a^{2}.$
Площадь круга:
$S= \pi \cdot R.$
