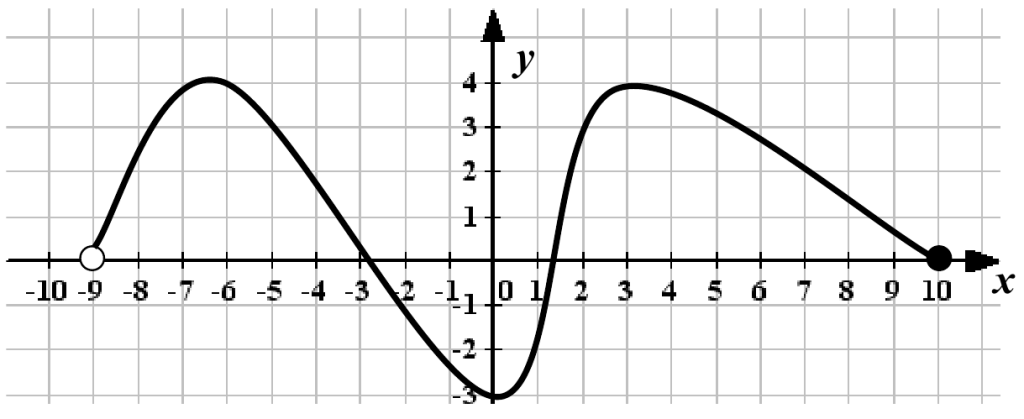
1. По графику функции определите:
а) области определения и значения функции;
б) промежутки возрастания и убывания функции;
в) точки экстремума функции.
2. Решите тригонометрические уравнения:
a) $\sqrt{2}\sin{2x}=0$;
б) $\rm{tg}$ $2x-1=0$.
3. Определите промежутки возрастания и убывания функции, используя производную:
$f(x)=\frac{x^{3}}{3}-2,5x^{2}+6x+10$
4. В треугольной пирамиде в основании лежит правильный треугольник со стороной равной $4$ м, а одно из боковых рёбер перпендикулярно плоскости основания, а другие образуют угол $30^{\circ}$ с плоскостью основания. Найдите объём пирамиды.
5. Квадрат со стороной равной $10$ см вращается вокруг одной из сторон. Найдите площадь поверхности получившегося тела вращения.
6. Найдите площадь фигуры, ограниченной линиями (предварительно сделайте рисунок):
$y=2x-x^{2}$ и $y=0$.
7. Решите неравенство:
$8^{x} \leq \frac{1}{128}$.
8. Решите уравнения:
а) $\log_{5}{(x^{2}-26x+50)}=2$;
б) $\sqrt{2x-1}=2$.
9. Вычислите:
а) $\int\limits_{1}^{3}{(5x^{4}+4x^{3}+1)dx}$;
б) $\int\limits_{\frac{\pi}{6}}^{\frac{\pi}{4}}{\frac{1}{\sin^{2}{x}}dx}$.
[ddownload id="447"]