Содержание
Понятие о тригонометрическом уравнении.
Определение.
Уравнение называется тригонометрическим, если в нём содержится любая тригонометрическая функция.
Например, уравнения $\sin{x} — 1 = 0$, $1-2\cos{x}=4$ и $\sqrt{3}\sin{x}-2\cos{x}=0$ тригонометрические, а $2-x=0$ — нет.
В силу того, что тригонометрическая функция периодична, тригонометрические уравнения имеют множество решений или не имеют их вообще.
Определение.
Под решением тригонометрического уравнения понимается такой набор чисел $x$, который при подстановке в уравнение обращает его в тождество.
Существуют 2 основных способа решения тригонометрических уравнений:
- графический способ, который заключается в том, что строятся графики левой и правой части уравнения и ищутся точки их пересечения;
- аналитический способ, суть которого заключается в применении специальных формул.
Простейшие тригонометрические уравнения.
Определение.
Под простейшими тригонометрическими уравнениями мы будем понимать тригонометрические уравнения, в левую часть которых входит только либо синус, либо косинус, а в правую — одно из чисел: $-1; \ 0; \ 1$.
Решим несколько простейших тригонометрических уравнений.
1. $\sin{x} = 1$
Начертим два графика: $y=\sin{x}$ и $y=1$
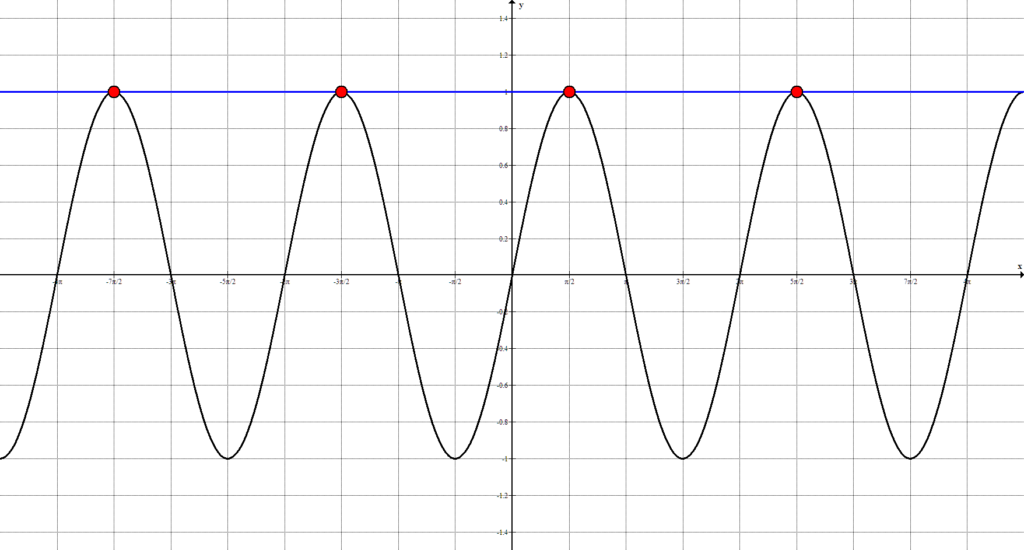
Видим, что количество точек пересечения достаточно велико, а, значит, необходимо выявить закономерность. Так как тригонометрические функции являются периодическими, то все точки, попавшие на 1-ый положительный период, будут периодически повторятся. Рассмотрим решения, попавшие на 1-ый период:
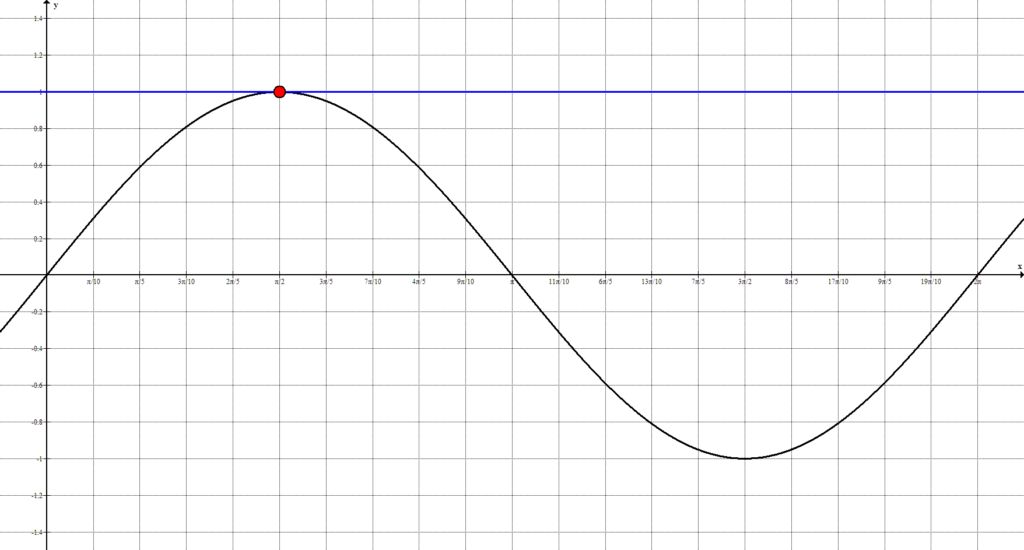
Это только одна точка: $\frac{\pi}{2}$. Периодом синуса является $2\pi$, так что получаем ответ:
$x = \frac{\pi}{2} + 2\pi n, \ n \in \mathbb{Z}$.
2. $\cos{x} = 0$
Начертим два графика: $y=\cos{x}$ и $y=0$
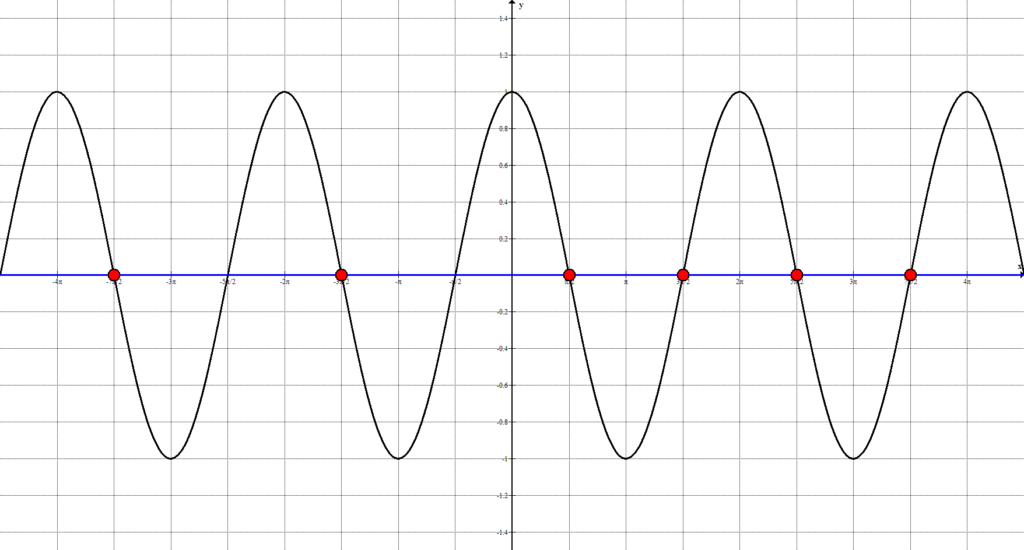
Видим, что количество точек пересечения достаточно велико, а, значит, необходимо выявить закономерность. Так как тригонометрические функции являются периодическими, то все точки, попавшие на 1-ый положительный период, будут периодически повторятся. Рассмотрим решения, попавшие на 1-ый период:
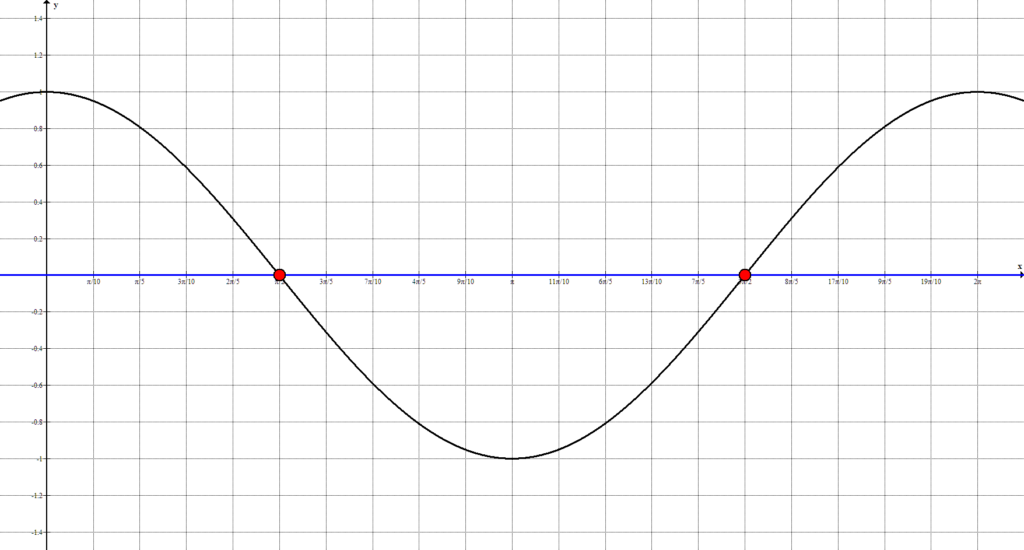
Видим, что получается 2 решения, попадающих «на период»: $x_{1}=\frac{\pi}{2}$ и $x_{2}=\frac{3\pi}{2}$.
Замечание.
Две точки решения получаются только у функций синус и косинус. Так как тангенс и котангенс монотонные (и на периоде в том числе), то они имеют лишь только одну точку пересечения с прямой $y=a$.
Получены два решения:
\(\left\{ \begin{array}{c} x_{1} = \frac{\pi}{2} + 2\pi n, \\ x_{2} = \frac{3\pi}{2} + 2\pi n, \end{array} \right. \)
которые можно попытаться объединить в одно.
Замечание.
Не все решения можно объединить в одно. Если это невозможно, то в ответ выписываются 2 решения.
Проверим расстояние между всеми точками (обычно достаточно проверить расстояние между 4 точками), чтобы убедиться, что объединение возможно. Несложно увидеть, что в нашем случае оно всегда равно $\pi$. Тогда наши решения объединяются в одно и мы получаем ответ:
$x = \frac{\pi}{2} + \pi n, \ n \in \mathbb{Z}$
Таблица решений простейших тригонометрических уравнений.
| Уравнение | $f(x) = \sin{x}$ | $f(x) = \cos{x}$ |
|---|---|---|
| $f(x)=1$ | $x = \frac{\pi}{2} + 2\pi n$ | $x =2\pi n$ |
| $f(x)=0$ | $x = \pi n$ | $x = \frac{\pi}{2} + \pi n$ |
| $f(x)=-1$ | $x = - \frac{\pi}{2} + 2\pi n$ | $x = \pi + 2\pi n$ |
Ограничения тригонометрических уравнений.
Очевидно, что тригонометрические функции $\tg$ и $\ctg$ в силу неограниченности по области значений и монотонности всегда имеют одно решение для любого $a$.
А для тригонометрических функций $\sin$ и $\cos$ справедливы следующие утверждения.
Утверждение
Если $|a| > 1$, то не существует решений тригонометрического уравнения $\sin{x} = a$ или $\cos{x} = a$.
Действительно, так как область значения тригонометрических функций $\sin$ и $\cos$ является отрезком $[-1;1]$, то любая прямая, лежащая выше прямой $y=1$ и ниже прямой $y = -1$, не будет пересекать график тригонометрических функций.
Утверждение
Если $|a| = 1$, то тригонометрические уравнения $\sin{x} = a$ или $\cos{x} = a$ имеют ровно одно решение на полуинтервале $[0;2\pi)$ (далее, периоде).
Действительно, прямая $y=1$ и прямая $y = -1$ пересекают графики тригонометрических функций ровно в одной точке.
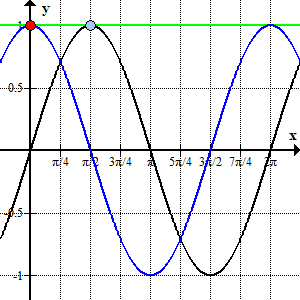
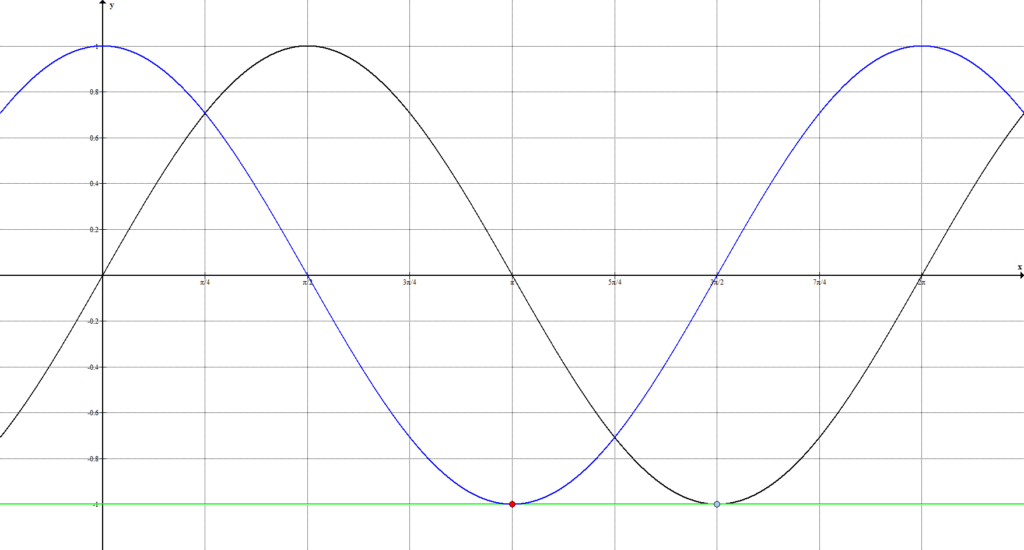
Утверждение
Если $|a| < 1$, то тригонометрические уравнения $\sin{x} = a$ или $\cos{x} = a$ имеют ровно два решения на периоде.
Действительно, прямая $y=a$ пересекает графики тригонометрических функций ровно в двух точках.
