Решаем неравенство с синусом

Большинство студентов тригонометрические неравенства недолюбливают. А зря. Как говаривал один персонаж,

«Вы просто не умеете их готовить»

Так как же «готовить» и с чем подавать неравенство с синусом мы разберёмся в этой статье. Решать мы будем самым простым способом — с помощью единичной окружности.

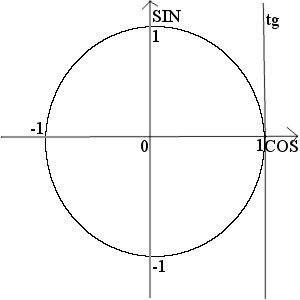
Итак, перво-наперво нам потребуется следующий алгоритм.

Алгоритм решения неравенств с синусом:

1. на оси синуса откладываем число $a$ и проводим прямую параллельно оси косинусов до пересечения с окружностью;
2. точки пересечения этой прямой с окружностью будут закрашенными, если неравенство нестрогое, и не закрашенными, если неравенство строгое;
3. область решения неравенства будет находится выше прямой и до окружности, если неравенство содержит знак «$>$», и ниже прямой и до окружности, если неравенство содержит знак «$<$»;
4. для нахождения точек пересечения, решаем тригонометрическое уравнение $\sin{x}=a$, получаем $x=(-1)^{n}\arcsin{a} + \pi n$;
5. полагая $n=0$, мы находим первую точку пересечения (она находится или в первой, или в четвёртой четверти);
6. для нахождения второй точки, смотрим, в каком направлении мы идём по области ко второй точке пересечения: если в положительном направлении, то следует брать $n=1$, а, если в отрицательном, то $n=-1$;
7. в ответ выписывается промежуток от меньшей точки пересечения $+ 2\pi n$ до большей $+ 2\pi n$.

Ограничение алгоритма

Важно: данный алгоритм не работает для неравенств вида $\sin{x} > 1; \ \sin{x} \geq 1, \ \sin{x} < -1, \ \sin{x} \leq -1$. В строгом случае эти неравенства не имеют решений, а в нестрогом — решение сводится к решению уравнения $\sin{x} = 1$ или $\sin{x} = -1$.

Частные случаи при решении неравенства с синусом

Важно отметить также следующие случаи, которые гораздо удобнее решить логически, не используя вышеуказанный алгоритм.

Частный случай 1. Решить неравенство:

$\sin{x} \leq 1.$

В силу того, что область значения тригонометрической функции $y=\sin{x}$ не больше по модулю $1$, то левая часть неравенства при любом $x$ из области определения (а область определения синуса — все действительные числа) не больше $1$. А, значит, в ответ мы записываем: $x \in R$.

Следствие: аналогично решается и неравенство

$\sin{x} \geq -1.$

Частный случай 2. Решить неравенство:

$\sin{x} < 1.$

Применяя аналогичные частному случаю 1 рассуждения, получим, что левая часть неравенства меньше $1$ для всех $x \in R$, кроме точек, являющихся решением уравнения $\sin{x} = 1$. Решая это уравнение, будем иметь:

$x = (-1)^{n}\arcsin{1}+ \pi n = (-1)^{n}\frac{\pi}{2} + \pi n.$

А, значит, в ответ мы записываем: $x \in R \backslash \left\{(-1)^{n}\frac{\pi}{2} + \pi n\right\}$.

Следствие: аналогично решается и неравенство

$\sin{x} > -1.$

Примеры решения неравенств с помощью алгоритма.

Пример 1: Решить неравенство:

$\sin{x} \geq \frac{1}{2}.$

1. Отметим на оси синусов координату $\frac{1}{2}$.
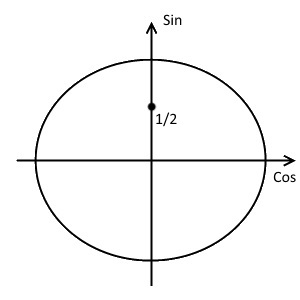
2. Проведём прямую параллельно оси косинусов и проходящую через эту точку.
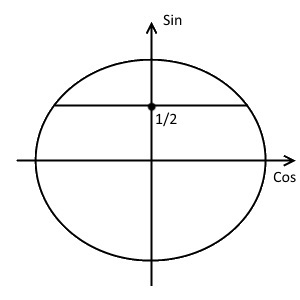
3. Отметим точки пересечения. Они будут закрашенными, так как неравенство нестрогое.
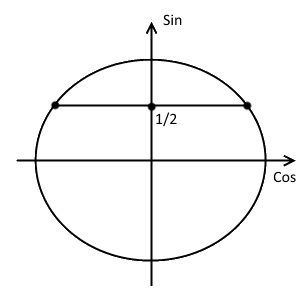
4. Знак неравенства $\geq$, а значит закрашиваем область выше прямой, т.е. меньший полукруг.
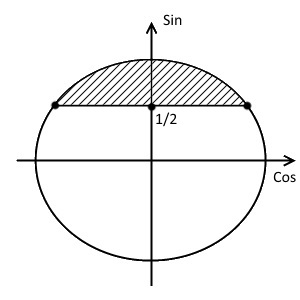
5. Находим первую точку пересечения. Для этого неравенство превращаем в равенство и решаем его: $\sin{x}=\frac{1}{2} \ \Rightarrow \ x=(-1)^{n}\arcsin{\frac{1}{2}}+\pi n =(-1)^{n}\frac{\pi}{6} + \pi n$. Полагаем далее $n=0$ и находим первую точку пересечения: $x_{1}=\frac{\pi}{6}$.
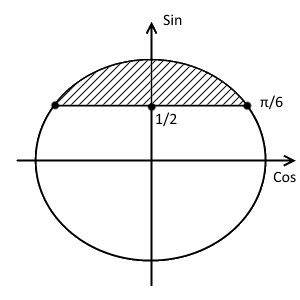
6. Находим вторую точку. Наша область идёт в положительном направлении от первой точки, значит $n$ полагаем равным $1$: $x_{2}=(-1)^{1}\frac{\pi}{6} + \pi \cdot 1 = \pi — \frac{\pi}{6} = \frac{5\pi}{6}$.

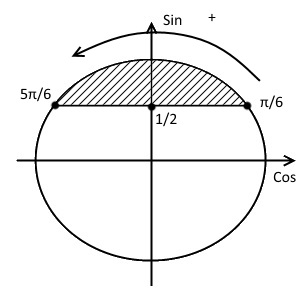
Таким образом, решение примет вид:

$x \in \left[\frac{\pi}{6} + 2\pi n; \frac{5\pi}{6} + 2 \pi n\right], \ n \in Z.$

Пример 2: Решить неравенство:

$\sin{x} < -\frac{1}{2}$

Отметим на оси синусов координату $- \frac{1}{2}$ и проведём прямую параллельно оси косинусов и проходящую через эту точку. Отметим точки пересечения. Они будут не закрашенными, так как неравенство строгое. Знак неравенства $<$, а, значит, закрашиваем область ниже прямой, т.е. меньший полукруг. Неравенство превращаем в равенство и решаем его:

$\sin{x}=-\frac{1}{2}$

$x=(-1)^{n}\arcsin{\left(-\frac{1}{2}\right)}+ \pi n =(-1)^{n+1}\frac{\pi}{6} + \pi n$.

Полагая далее $n=0$, находим первую точку пересечения: $x_{1}=-\frac{\pi}{6}$. Наша область идёт в отрицательном направлении от первой точки, значит $n$ полагаем равным $-1$: $x_{2}=(-1)^{-1+1}\frac{\pi}{6} + \pi \cdot (-1) = -\pi + \frac{\pi}{6} = -\frac{5\pi}{6}$.

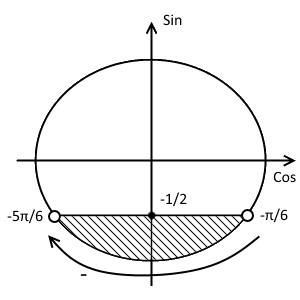Итак, решением этого неравенства будет промежуток:

$x \in \left(-\frac{5\pi}{6} + 2\pi n; -\frac{\pi}{6} + 2 \pi n\right), \ n \in Z.$

Пример 3: Решить неравенство:

$1 — 2\sin{\left(\frac{x}{4}+\frac{\pi}{6}\right)} \leq 0.$

Этот пример решать сразу с помощью алгоритма нельзя. Для начала его надо преобразовать. Делаем в точности так, как делали бы с уравнением, но не забываем про знак. Деление или умножение на отрицательное число меняет его на противоположный!

Итак, перенесём всё, что не содержит тригонометрическую функцию в правую часть. Получим:

$- 2\sin{\left(\frac{x}{4}+\frac{\pi}{6}\right)} \leq -1.$

Разделим левую и правую часть на $-2$ (не забываем про знак!). Будем иметь:

$\sin{\left(\frac{x}{4}+\frac{\pi}{6}\right)} \geq \frac{1}{2}.$

Опять получилось неравенство, которое мы не можем решить с помощью алгоритма. Но здесь уже достаточно сделать замену переменной:

$t=\frac{x}{4}+\frac{\pi}{6}.$

Получаем тригонометрическое неравенство, которое можно решить с помощью алгоритма:

$\sin{t} \geq \frac{1}{2}.$

Это неравенство было решено в примере 1, поэтому позаимствуем оттуда ответ:

$t \in \left[\frac{\pi}{6} + 2\pi n; \frac{5\pi}{6} + 2 \pi n\right].$

Однако, решение ещё не закончилось. Нам нужно вернуться к исходной переменной.

$(\frac{x}{4}+\frac{\pi}{6}) \in \left[\frac{\pi}{6} + 2\pi n; \frac{5\pi}{6} + 2 \pi n\right].$

Представим промежуток в виде системы:

$\left\{\begin{array}{c} \frac{x}{4}+\frac{\pi}{6} \geq \frac{\pi}{6} + 2\pi n, \\ \frac{x}{4}+\frac{\pi}{6} \leq \frac{5\pi}{6} + 2 \pi n. \end{array} \right.$

В левых частях системы стоит выражение ($\frac{x}{4}+\frac{\pi}{6}$), которое принадлежит промежутку. За первое неравенство отвечает левая граница промежутка, а за второе — правая. Причём скобки играют немаловажную роль: если скобка квадратная, то неравенство будет нестрогим, а если круглая, то строгим. наша задача получить слева $x$ в обоих неравенствах.

Перенесём $\frac{\pi}{6}$ из левой части в правые, получим:

$\left\{\begin{array}{c} \frac{x}{4} \geq \frac{\pi}{6} + 2\pi n -\frac{\pi}{6}, \\ \frac{x}{4} \leq \frac{5\pi}{6} + 2 \pi n — \frac{\pi}{6}. \end{array} \right.$

Упрощая, будем иметь:

$\left\{\begin{array}{c} \frac{x}{4} \geq 2\pi n, \\ \frac{x}{4} \leq \frac{2\pi}{3} + 2 \pi n. \end{array} \right.$

Умножая левые и правые части на $4$, получим:

$\left\{\begin{array}{c} x \geq 8\pi n, \\ x \leq \frac{8\pi}{3} + 8 \pi n. \end{array} \right.$

Собирая систему в промежуток, получим ответ:

$x \in \left[ 8\pi n; \frac{8\pi}{3} + 8 \pi n\right], \ n \in Z.$