Перед вами третья статья из цикла «Геометрические преобразования графиков функций«.
1. Растяжение в $|k_1|$ раз по оси $Ox$.
Правило:
Чтобы построить график функции $y=f(|k_{1}|x)$, необходимо каждому значению функции $y=f(x)$, вычисленному в точке с абсциссой $x_{0}$, сопоставить абсциссу $\frac{x_{0}}{|k_{1}|}$.
Рассмотрим это преобразование на примерах.
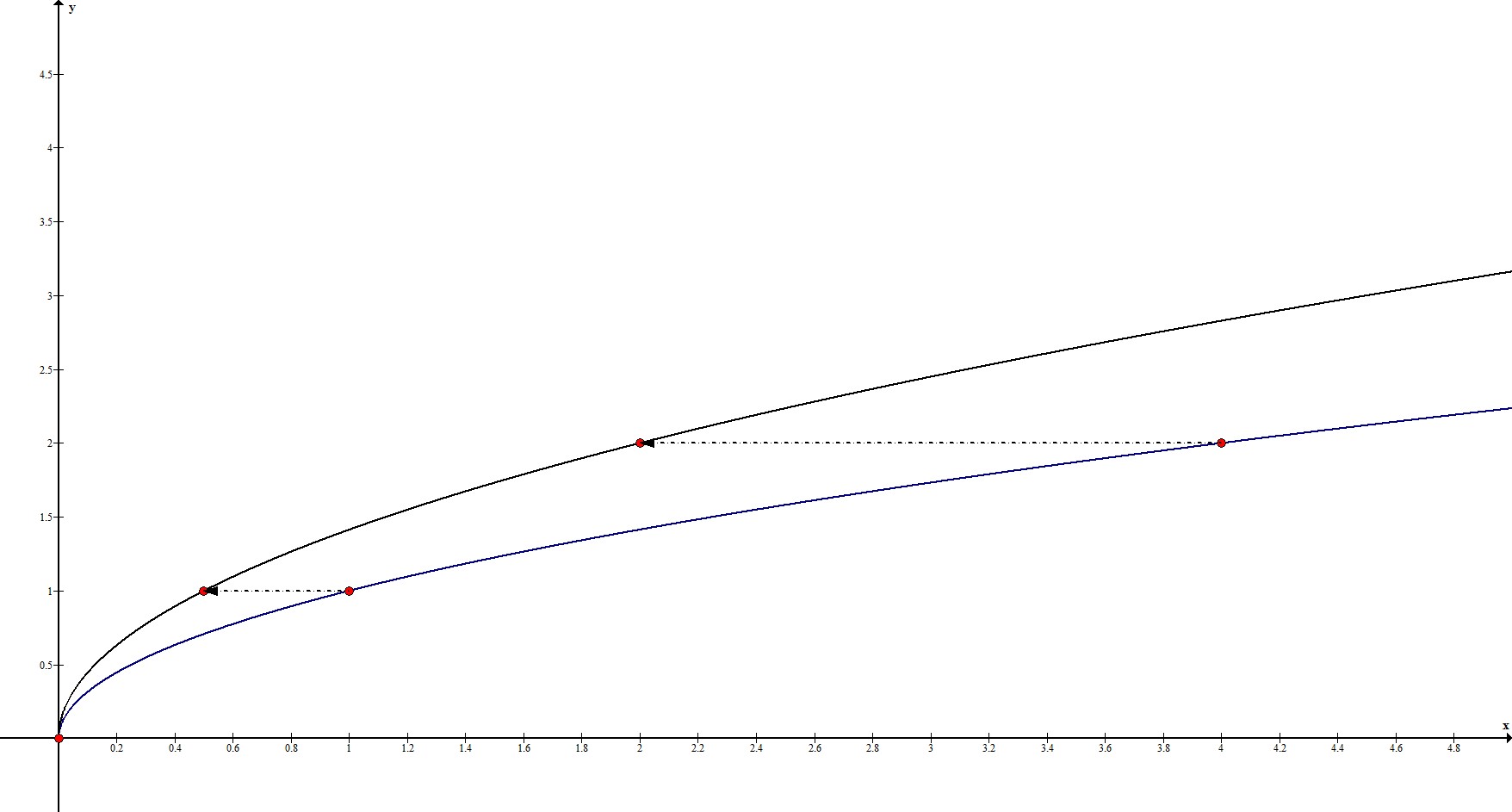
1. $y=\sqrt{2x}$
Прообразом этой функции будет $y_0=\sqrt{x}$.
$|k_1|=2 \neq 1 \Rightarrow$ происходит растяжение в 2 раза по оси $Ox$.
Рассмотрим ключевые точки функции: $(0;0), \ (1;1), \ (4;2)$.
Сопоставим значению прообраза в каждой ключевой координате абсциссу $\frac{x_0}{2}$, то есть:
$(0;0) \rightarrow x=\frac{0}{2}=0; y=0 \rightarrow (0;0)$;
$(1;1) \rightarrow x=\frac{1}{2}=0,5; y=1 \rightarrow (0,5;1)$;
$(4;2) \rightarrow x=\frac{4}{2}=2; y=2 \rightarrow (2;2)$.
То есть, наши ключевые точки переходят в точки $(0;0), \ (0,5;1), \ (2;2)$.
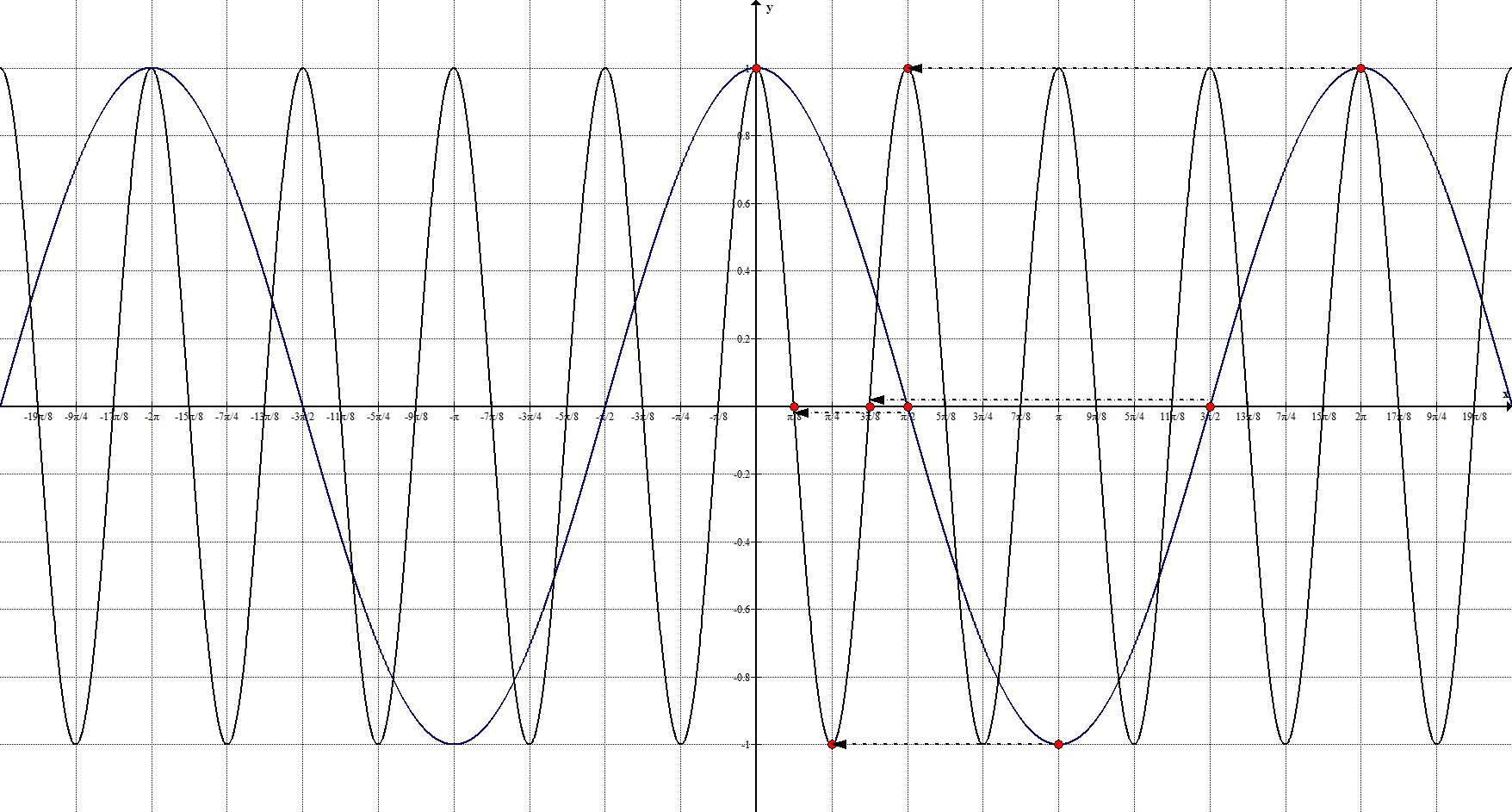
2. $y=\cos{4x}$
Прообразом этой функции будет $y_0=\cos{x}$.
$|k_1|=4 \neq 1 \Rightarrow$ происходит растяжение в 4 раза по оси $Ox$.
Рассмотрим ключевые точки функции (возьмём ключевые точки первого положительного оборота):
$(0;1), \ \left(\frac{\pi}{2}; 0\right), \ (\pi;-1), \ \left(\frac{3\pi}{2}; 0\right), \ (2\pi; 1)$.
Сопоставим значению прообраза в каждой ключевой координате абсциссу $\frac{x_0}{2}$, то есть:
$(0;1) \rightarrow x=\frac{0}{4}=0; y=1 \rightarrow (0;1)$;
$\left(\frac{\pi}{2};0\right) \rightarrow x=\frac{\frac{\pi}{2}}{4}=\frac{\pi}{8}; y=0 \rightarrow \left(\frac{\pi}{8};0\right)$;
$\left(\pi;-1\right) \rightarrow x=\frac{\pi}{4}; y=-1 \rightarrow \left(\frac{\pi}{4};-1\right)$;
$\left(\frac{3\pi}{2};0\right) \rightarrow x=\frac{\frac{3\pi}{2}}{4}=\frac{3\pi}{8}; y=0 \rightarrow \left(\frac{3\pi}{8};0\right)$;
$\left(2\pi;1\right) \rightarrow x=\frac{2\pi}{4}=\frac{\pi}{2}; y=1 \rightarrow \left(\frac{\pi}{2};1\right)$.
Таким образом, нашими ключевыми точками становятся точки: $(0;1), \ \left(\frac{\pi}{8};0\right), \ \left(\frac{\pi}{4};-1\right), \ \frac{3\pi}{8} \rightarrow \left(\frac{3\pi}{8};0\right), \ \left(\frac{\pi}{2};1\right)$.
2. Растяжение в $|k_2|$ раз по оси $Oy$.
Правило:
Чтобы построить график функции $y=|k_{2}|f(x)$, необходимо значение функции $y=f(x)$ в каждой точке умножить на $|k_{2}|$ единиц.
Рассмотрим это преобразование на примерах.
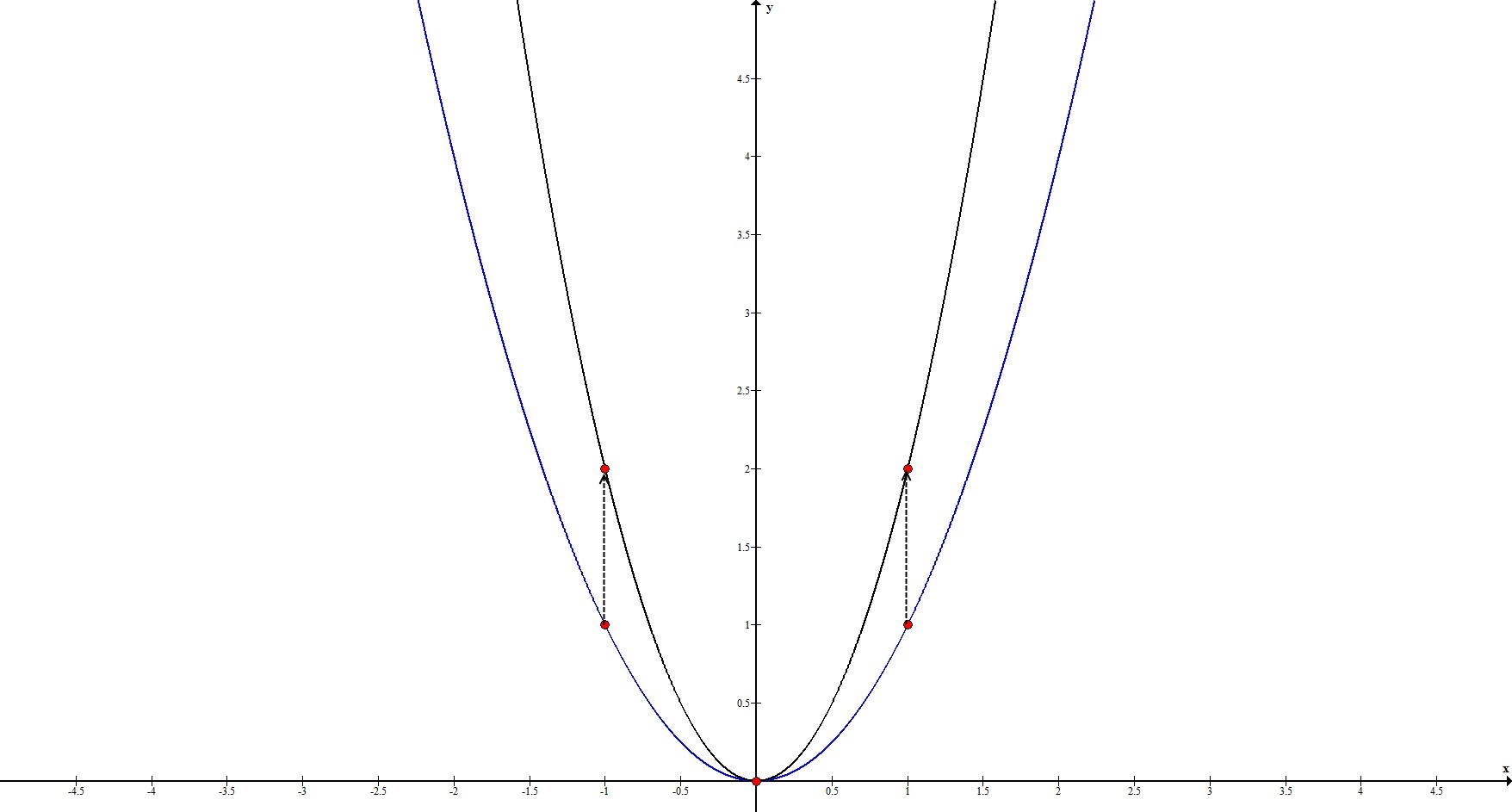
1. $y=2x^2$
Прообразом этой функции будет $y_0=x^2$.
$|k_2|=2 \neq 1 \Rightarrow$ происходит растяжение в 2 раза по оси $Oy$.
Рассмотрим ключевые точки функции: $(-1;1), \ (0;0), \ (1;1)$.
Значение функции в каждой этой точке умножается на 2, то есть:
$(-1;1) \rightarrow x=-1; y=2 \cdot 1 = 2 \rightarrow (-1;2)$;
$(0;0) \rightarrow x=0; y=2 \cdot 0 = 0 \rightarrow (0;0)$;
$(1;1) \rightarrow x=1; y=2 \cdot 1 = 2 \rightarrow (1;2)$.
Итак, имеем: $(-1;2), \ (0;0), \ (1;2)$.
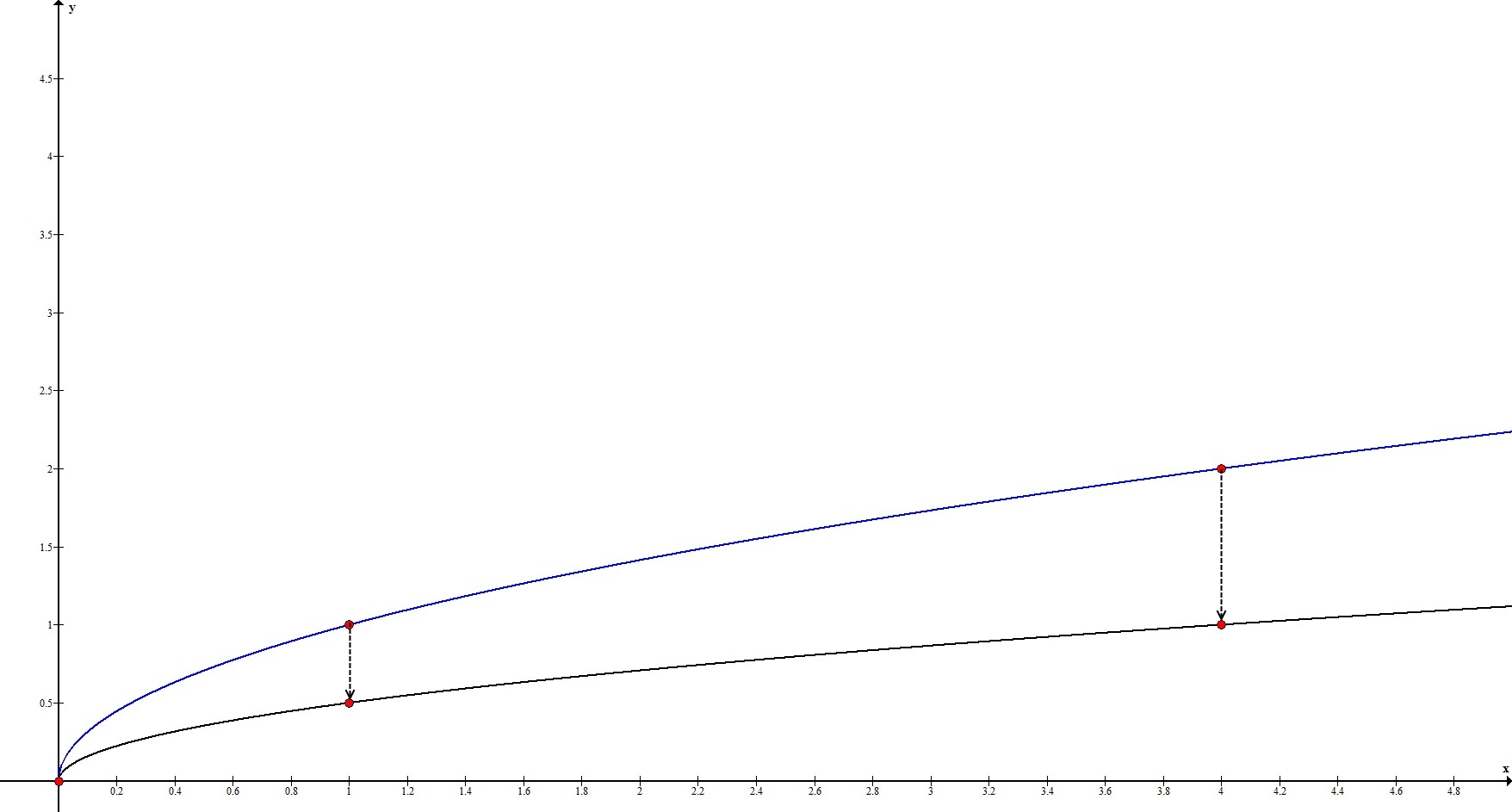
2. $y=0,5\sqrt{x}$
Прообразом этой функции будет $y_0=\sqrt{x}$.
$|k_2|=0,5 \neq 1 \Rightarrow$ происходит растяжение в 0,5 раза по оси $Oy$.
Рассмотрим ключевые точки функции: $(0;0), \ (1;1), \ (4;2)$.
Значение функции в каждой этой точке умножается на 0,5, то есть:
$(0;0) \rightarrow x=0; y=0,5 \cdot 0 = 0 \rightarrow (0;0)$;
$(1;1) \rightarrow x=1; y=0,5 \cdot 1 = 0,5 \rightarrow (1;0,5)$;
$(4;2) \rightarrow x=4; y=0,5 \cdot 2 = 1 \rightarrow (4;1)$.
Итак, имеем:
$(0;0), \ (1;0,5), \ (4;1)$.
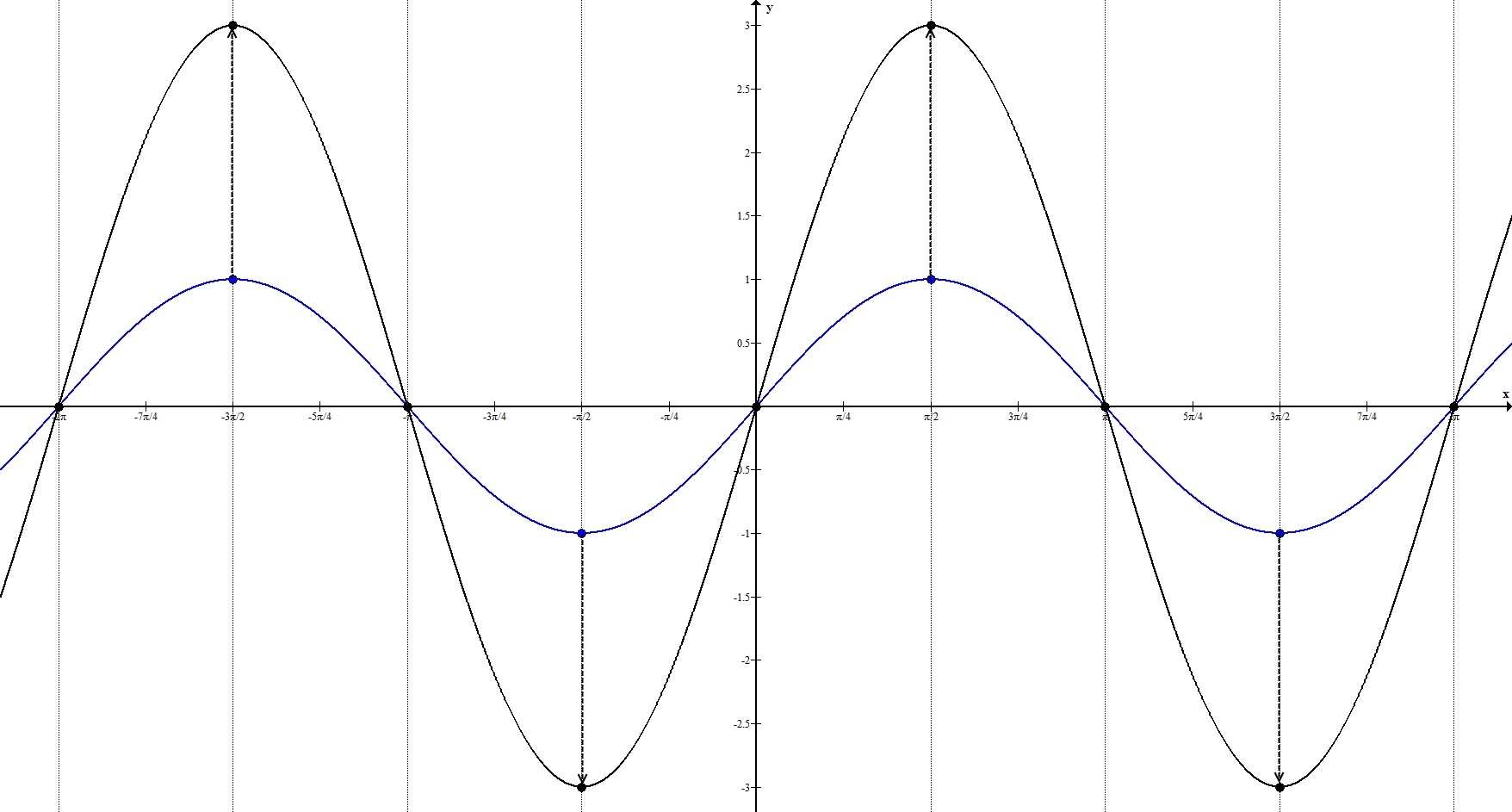
3. $y=3\sin{x}$
Прообразом этой функции будет $y_0=\sin{x}$.
$|k_2|=3 \neq 1 \Rightarrow$ происходит растяжение в 3 раза по оси $Oy$.
Рассмотрим ключевые точки функции (возьмём ключевые точки первого положительного оборота):
$(0;0), \ \left(\frac{\pi}{2}; 1\right), \ (\pi; 0), \ \left(\frac{3\pi}{2}; -1\right), \ (2\pi; 0)$
Значение функции в каждой этой точке умножается на 3, то есть:
$(0;0) \rightarrow x=0; y=3 \cdot 0 = 0 \rightarrow (0;0)$;
$\left(\frac{\pi}{2}; 1\right) \rightarrow x=\frac{\pi}{2}; y=3 \cdot 1 = 3 \rightarrow \left(\frac{\pi}{2}; 3\right)$;
$\left(\pi; 0\right) \rightarrow x=\pi; y=3 \cdot 0 = 0 \rightarrow \left(\pi; 0\right)$;
$\left(\frac{3\pi}{2}; -1\right) \rightarrow x=\frac{3\pi}{2}; y=3 \cdot (-1) = -3 \rightarrow \left(\frac{3\pi}{2}; -3\right)$;
$\left(2\pi; 0\right) \rightarrow x=2\pi; y=3 \cdot 0 = 0 \rightarrow \left(2\pi; 0\right)$.
Итак, имеем:
$(0;0), \ \left(\frac{\pi}{2}; 3\right), \ (\pi; 0), \ \left(\frac{3\pi}{2}; -3\right), \ (2\pi; 0)$
Замечание:
Как вы уже наверное отметили, при растяжении по оси $Oy$ есть точки, которые не меняются. Те точки, в которых $y=0$. Это свойство удобно применять при построении тригонометрических (и любых других периодических) функций.