Решаем неравенство с тангенсом

Как с косинусом и синусом, решать неравенства с тангенсом мы будем с помощью единичной окружности.

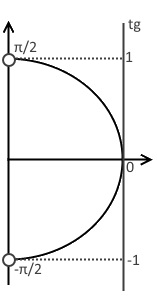
Алгоритм решения неравенств с тангенсом:

1. перерисовываем клише, изображённое на вышестоящем рисунке;
2. на линии тангенса отмечаем $a$ и проводим до этой точки из начала координат прямую;
3. точка пересечения этой прямой с полуокружностью будет закрашенной, если неравенство нестрогое и не закрашенное, если строгое;
4. область будет находится снизу от прямой и до окружности, если неравенство содержит знак «$>$», и снизу прямой и до окружности, если неравенство содержит знак «$<$»;
5. для нахождения точки пересечения, достаточно найти арктангенс $a$, т.е. $x_{1}={\rm arctg} a$;
6. в ответ выписывается полученный промежуток, добавляя к концам $+ \pi n$.

Примеры решения неравенств с помощью алгоритма.

Пример 1: Решить неравенство:

${\rm tg}{x} \leq 1.$

1. Копируем клише.
2. Отметим на линии тангенса координату $1$.
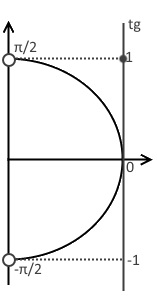
3. Проводим до этой точки из начала координат прямую.
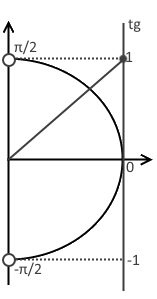
4. Отметим точку пересечения. Она будет закрашенной, так как неравенство нестрогое.
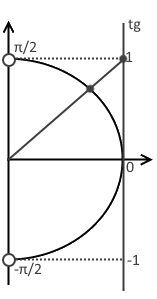
5. Знак неравенства $\leq$, а, значит, закрашиваем область снизу от прямой, т.е. больший «кусок пирога».
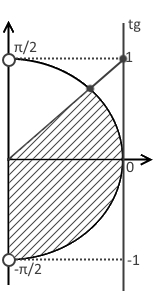
6. Находим точку пересечения: $x_{1}={\rm arctg}{1}=\frac{\pi}{4}$.

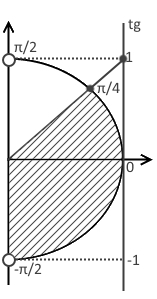
Таким образом, решение примет вид:

$x \in \left(-\frac{\pi}{2} + \pi n; \frac{\pi}{4} + \pi n\right], \ n \in Z.$

Важно! Точки $-\frac{\pi}{2}$ и $\frac{\pi}{2}$ у тангенса всегда (независимо от знака неравенства) выколоты!

Пример 2: Решить неравенство:

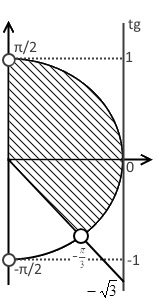
${\rm tg}{x} > — \sqrt{3}.$

Отмечаем на линии тангенса точку $- \sqrt{3}$ и проводим прямую из начала координат до неё. Точка пересечения этой прямой с полуокружностью будет не закрашенной, так как неравенство строгое. Область будет находится выше прямой и до окружности, так как знак неравенства $>$. найдём точку пересечения:

$x_{1} = {\rm arctg}{\left(-\sqrt{3}\right)} = -\frac{\pi}{3}.$

Таким образом, ответом будет:

$x \in \left(-\frac{\pi}{3} + \pi n; \frac{\pi}{2} + \pi n\right), \ n \in Z.$

Пример 3: Решить неравенство:

${\rm tg}{\left(2x-\frac{\pi}{3}\right)} + \sqrt{3} > 0.$

Сейчас применить алгоритм нельзя. Этот пример похож на пример 3 неравенства с синусом или косинусом. И действовать нужно аналогично. Сначала перенесём всё, что не содержит тригонометрической функции в правую часть.

${\rm tg}{\left(2x-\frac{\pi}{3}\right)} > — \sqrt{3}.$

Теперь же, чтобы применить алгоритм, делаем замену переменной. Всё, что стоит под тригонометрической функцией, обозначаем за новую переменную:

$t=2x-\frac{\pi}{3}$

и получаем неравенство

${\rm tg}{t} > — \sqrt{3},$

которое мы уже решили в примере 2:

$t \in \left(-\frac{\pi}{3} + \pi n; \frac{\pi}{2} + \pi n\right).$

Возвращаемся к исходной переменной:

$\left(2x-\frac{\pi}{3}\right) \in \left(-\frac{\pi}{3} + \pi n; \frac{\pi}{2} + \pi n\right).$

Последнее равносильно системе неравенств

$\left\{\begin{array}{c} 2x-\frac{\pi}{3} > -\frac{\pi}{3} + \pi n, \\ 2x-\frac{\pi}{3} < \frac{\pi}{2}+\pi n, \end{array} \right.$

решив которую мы получим ответ. Действительно,

$\left\{\begin{array}{c} 2x > \pi n, \\ 2x < \frac{5 \pi}{6} + \pi n, \end{array} \right.$

$\left\{\begin{array}{c} x > \frac{\pi n}{2}, \\ x < \frac{5\pi}{12}+\frac{\pi n}{2}. \end{array} \right. $

И окончательно получаем:

$x \in \left(\frac{\pi n}{2}; \frac{5\pi}{12} + \frac{\pi n}{2}\right), \ n \in Z.$