Условие: В цилиндре осевое сечение имеет площадь равную 100 см$^{2}$, а длина окружности основания равна $10pi$ см. Найдите его объём и площадь полной поверхности.
Решение:
Сделаем рисунок:
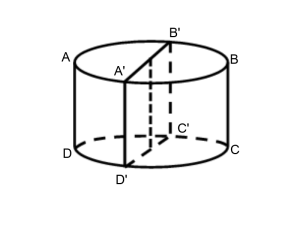 Дано: $ABCD$ — цилиндр, $A’B’C’D’$ — осевое сечение, $S_{A’B’C’D’}=100 $ см$^{2}$, $l=10 \pi$ см. Найти: $V, S$пп$ — ?$
Дано: $ABCD$ — цилиндр, $A’B’C’D’$ — осевое сечение, $S_{A’B’C’D’}=100 $ см$^{2}$, $l=10 \pi$ см. Найти: $V, S$пп$ — ?$
- $l=2pi R=10 pi Rightarrow R=frac{10 pi}{2 pi}=5$ (см);
- $A’B’=D=2R=2 cdot 5=10$ (см);
- $S_{A’B’C’D’}=A’B’cdot B’C’=10B’C’=10h=100 Rightarrow h=10$ (см);
- $V=pi R^{2}h=pi cdot 5^{2} cdot 10=250pi$ (см$^{3}$);
- $S$пп$=S$бп$+2S$осн;
- $S$бп$=2pi Rh=2 pi cdot 5 cdot 10=100 pi$ (см$^{2}$);
- $S$осн$=pi R^{2}=25 pi$ (см$^{2}$);
- $S$пп$=100pi +2cdot 25pi = 150pi$ (см$^{2}$).
Ответ: $V=250pi$ см$^{3}$, $S$пп$=150pi$ см$^{2}$.
