Теория.
Для начала рекомендуется ознакомится со статьёй «Логарифм и его свойства«, описывающей теорию про логарифмы, и статьёй «Решение простейших логарифмических уравнений«, описывающей методы решения логарифмических уравнений.
Неравенство называется логарифмическим, если в нём содержится логарифмическая функция.
Методы решения логарифмических неравенств не отличаются от методов решений логарифмических уравнений, за исключением двух вещей.
Во-первых, при переходе от логарифмического неравенства к неравенству подлогарифмических функций следует следить за знаком получающегося неравенства. Он подчиняется следующему правилу.
Если основание логарифмической функции больше $1$, то при переходе от логарифмического неравенства к неравенству подлогарифмических функций знак неравенства сохраняется, а если же меньше $1$, то меняется на противоположный.
Во-вторых, решение любого неравенства — промежуток, а, значит, в конце решения неравенства подлогарифмических функций необходимо составить систему из двух неравенств: первым неравенством этой системы будет неравенство подлогарифмических функций, а вторым — промежуток области определения логарифмических функций, входящих в логарифмическое неравенство.
Практика.
Решим неравенства:
1. $\log_{2}{(x+3)} \geq 3.$
Для начала найдём область определения:
$D(y): \ x+3>0.$
$\ x>-3$
$x \in (-3;+\infty)$
Основание логарифма равно $2>1$, поэтому знак не меняется. Пользуясь определением логарифма, получим:
$x+3 \geq 2^{3},$
$x+3 \geq 8,$
$x \geq 5,$
$x \in [5; + \infty).$
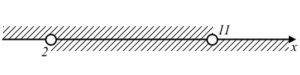
Соединяя полученное решение с областью определения, получим: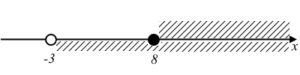
Ответ: $x \in [5; +\infty)$.
2. $\log_{\frac{1}{3}}{(x-2)} > -2.$
Для начала найдём область определения:
$D(y): \ x-2>0.$
$\ x>2$
$x \in (2;+\infty)$
Основание равно $\frac{1}{3}<1$, а, значит, знак неравенства меняется на противоположный. Получаем:
$x-2<\left(\frac{1}{3}\right)^{-2},$
$x-2<9,$
$x<11,$
$x \in (- \infty; 11).$
Соединяя полученное решение с областью определения, получим:
Ответ: $x \in (2; 11).$
Разберём теперь более сложный пример из задания C1 экзамена.
3. $\log_{3}{(2x+1)} \geq \log_{\frac{1}{3}}{\left(\frac{1}{7-x}\right)}$.
Для начала найдём область определения:
$D(y): \ 2x+1>0, \ \frac{1}{7-x}>0, \ 7-x \neq 0,$
$2x+1>0, \ 7-x>0, \ 7-x \neq 0,$
таким образом, третье неравенство излишне (второе уже не допускает равенства!) , получим:
$x>-0,5, \ x<7,$
$x \in (-0,5;7).$
Преобразуем логарифм, стоящий в правой части, используя пятое и шестое свойство из статьи «Логарифм и его свойства«.
$\log_{\frac{1}{3}}{\left(\frac{1}{7-x}\right)}=\frac{1}{-1}\log_{3}{\left(\frac{1}{7-x}\right)}=-\log_{3}{\left(\frac{1}{7-x}\right)}=\log_{3}{\left(\frac{1}{7-x}\right)^{-1}}=$
$=\log_{3}{(7-x)}.$
Таким образом, получено следующее неравенство:
$\log_{3}{(2x+1)} \geq \log_{3}{(7-x)}$.
Основание равно $3>1$, а, значит, знак неравенства не меняется. Получаем:
$2x+1 \geq 7-x,$
$3x \geq 6,$
$x \geq 2,$
$x \in [2; +\infty).$
Соединяя полученное решение с областью определения, получаем ответ.
Ответ: $x \in [2; 7).$